Kapitel 1 : Potenzen
1.0 Überblick
1.1 Potenzen mit ganzzahligen Exponenten
1.2 Potenzen mit gleichen Basen
1.3 Potenzen mit gleichen Exponenten
1.4 Wurzeln
1.5 Potenzen mit rationalen Exponenten
Quellen
Lambacher Schweizer: "Mathematik für Gymnasien Klasse 10" [ISBN: 978-3-12-734291-8]Lambacher Schweizer Mathematik 10. Klasse
1.4 Wurzeln
Motivation für Wurzeln: Umkehrung der Potenzen
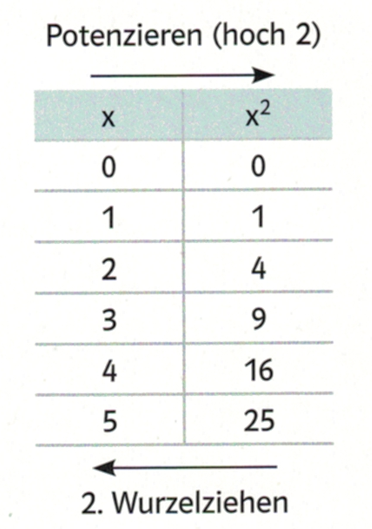
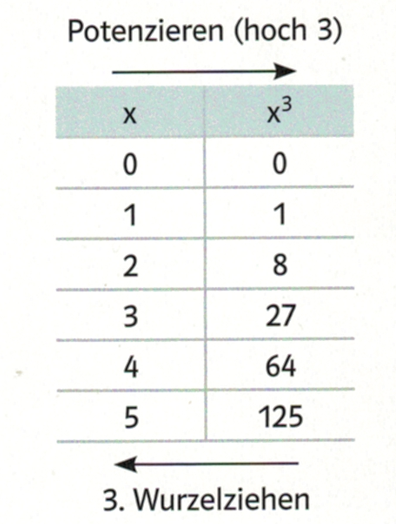
Definition: Ist $a = b^2$ mit $b \geq 0 $ , dann heisst b die "zweite Wurzel"(oder "Quadratwurzel") aus a:
$a = b^2 ~~\big\vert~~\sqrt[2]{b}$ : auf beiden Seiten 2. Wurzel ziehen
$\sqrt[2]{a} = \sqrt[2]{b^2}$
$\boxed{\sqrt[2]{a} = \sqrt{a} = b}$
Definition: Ist $a = b^3$ mit $b \geq 0 $ , dann heisst b die "dritte Wurzel" aus a:
$a = b^3 ~~\big\vert~~\sqrt[3]{b}$ : auf beiden Seiten 3. Wurzel ziehen
$\sqrt[3]{a} = \sqrt[3]{b^3}$
$\boxed{\sqrt[3]{a} = b}$
Definition: Kurzschreibweise:
$\boxed{\sqrt[k]{x} := x^{(\dfrac{1}{k})}}$ : Wurzeln können mit Potenzen berechnet werden!
Aufgabe: Berechne $T = \sqrt[4]{10000}$
$T = \sqrt[4]{10000} = \sqrt[4]{10 \cdot 10 \cdot 10 \cdot 10} = 10$
Aufgabe: Berechne $T = 27^{(\dfrac{1}{3})}$
$T = 27^{(\dfrac{1}{3})} ~~\big\vert~~()^3$
$T^3 = (27^{(\dfrac{1}{3})})^3 = 27$
$T^3 = T \cdot T \cdot T = 3 \cdot 3 \cdot 3 \Rightarrow \boxed{T = 3}$
Homepage WebSites Unterrichtsstunden Mathematik