Kapitel 1 : Lineare Gleichungssysteme
1.0 Überblick
1.1 Lösung linearer Gleichungssysteme
1.2 Lineare Gleichungen mit zwei Variablen
1.3 Lineare Gleichungssystem grafisch lösen
1.4 Lösen von linearen Gleichungssystemen ohne CAS
1.5 Lösen von linearen Gleichungssystemen mit CAS
1.6 Anwendungen
1.7 Einfache Aufgaben
1.8 Lösungsverfahren
Quellen
Lambacher Schweizer: "Mathematik für Gymnasien Klasse 9" [ISBN: 978-3-12-734291-8]Klett Verlag : Lambacher Schweizer Mathematik 9
1.8 Lösungsverfahren
Formalisierung des Problems
GegebenZwei Geraden (1) und (2) mit gegebenen Koeffizienten $a,b,c,u,v,w$ und den zu bestimmenden Unbekannten $x,y$ :
$\boxed{ax + by = c~}$ (1) mit gegebenen $a,b,c \in \mathbb{R}$ und $x,y \in \mathbb{R}$
$\boxed{ux + vy = w}$ (2) mit gegebenen $u,v,w \in \mathbb{R}$
Gesucht
Gesucht wird der gemeinsame Schnittpunkt $P_s$ beider Geraden (1) und (2) mit:
$\boxed{P_s = (x_s,y_s)}$ (3) mit $x_s,y_s \in \mathbb{R}$
Lösung
Wir lernen hier drei Verfahren zur Berechnung des Schnittpunktes $P_s=(x_s,y_s)$ zweier Geraden () und () kennen:
• Gleichsetzungsverfahren
• Einsetzungsverfahren
• Additionsverfahren
• Allgemeines Analytisches Verfahren
• Determinantenverfahren
Gleichsetzungsverfahren
Gegebensei das folgende lineare Gleichungssystem:
$\boxed{2x + 7y = 14}$ (11)
$\boxed{3x + 2y = 12}$ (12)
Grafik
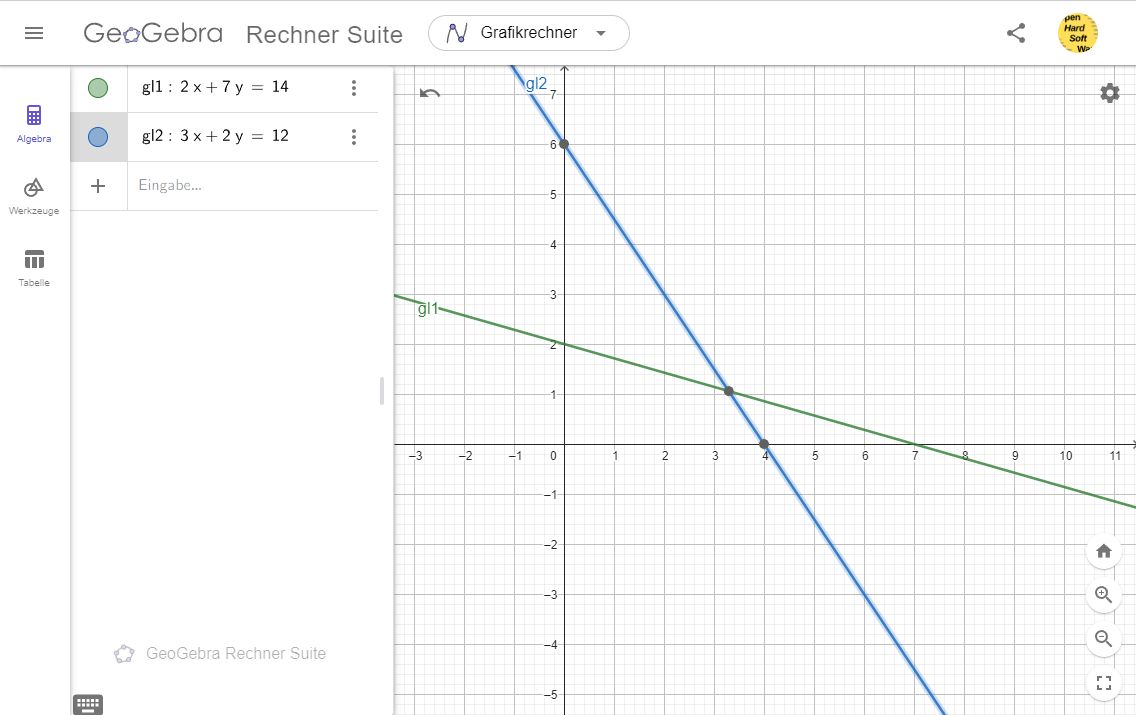
Aufgabe
Berechne $x_s$ und $y_s$ des gemeinsamen Schnittpunktes $\boxed{P_s=(x_s,y_s)}$
Lösung
Forme (11) und (12) nach $y=...$ um:
$2x + 7y = 14$ (*11)
$7y = -2x + 14$
$y = -\dfrac{2}{7}x + \dfrac{14}{7}$
$\boxed{y = -\dfrac{2}{7}x + 2}$ (13)
$3x + 2y = 12$ (*12)
$2y = - 3x + 12$
$y = -\dfrac{3}{2}x + \dfrac{12}{2}$
$\boxed{y = -\dfrac{3}{2}x + 6}$ (14)
Setze (13) und (14) gleich und eleminiere damit $y$ :
$-\dfrac{2}{7}x + 2 = -\dfrac{3}{2}x + 6$
Auflösung nach $x$ :
$-2x + 14 = -\dfrac{21}{2}x + 42$
$-4x + 28 = -21x + 84$
$21x -4x + 28 = 84$
$17x = 56$
Schnittstelle $x_s$ des Schnittpunkts beider Geraden (11) und (12):
$\boxed{x = x_s = \dfrac{56}{17} = 3\dfrac{5}{17}}$ (15)
Setze Gleichung (15) in eine der Bestimmungsgleichungen (13) oder (14) für $y$ ein.
Dies ist deine Wahl, beide Bestimmungsgleichungen sind gleichwertig!
Wir nehmen hier (13):
$y = -\dfrac{2}{7}x + 2$ (*13)
$y = -\dfrac{2}{7} \cdot \dfrac{56}{17} + 2$
$y = -2 \cdot \dfrac{8}{17} + 2$
$y = -\dfrac{16}{17} + \dfrac{34}{17}$
$\boxed{y = y_s = \dfrac{18}{17} = 1\dfrac{1}{17}}$ (16)
Mit dem Gleichsetzungsverfahren bestimmt sich der Schnittpunkt:
$\boxed{P_s=(x_s,y_s) = (\dfrac{56}{17}, \dfrac{18}{17}) = (3\dfrac{5}{17},1\dfrac{1}{17})}$ (17)
als Lösung des linearen Gleichungssystems:
$\boxed{2x + 7y = 14}$ (*11)
$\boxed{3x + 2y = 12}$ (*12)
Einsetzungsverfahren
Gegebensei das folgende lineare Gleichungssystem:
$\boxed{3x + y = 5\frac{1}{3}}$ (21)
$\boxed{y = 2x +\dfrac{1}{3}}$ (22)
Bemerkung: jede Geradengleichung kann ich wie (22) auf die Form $y = mx + c$ bringen !
Grafik
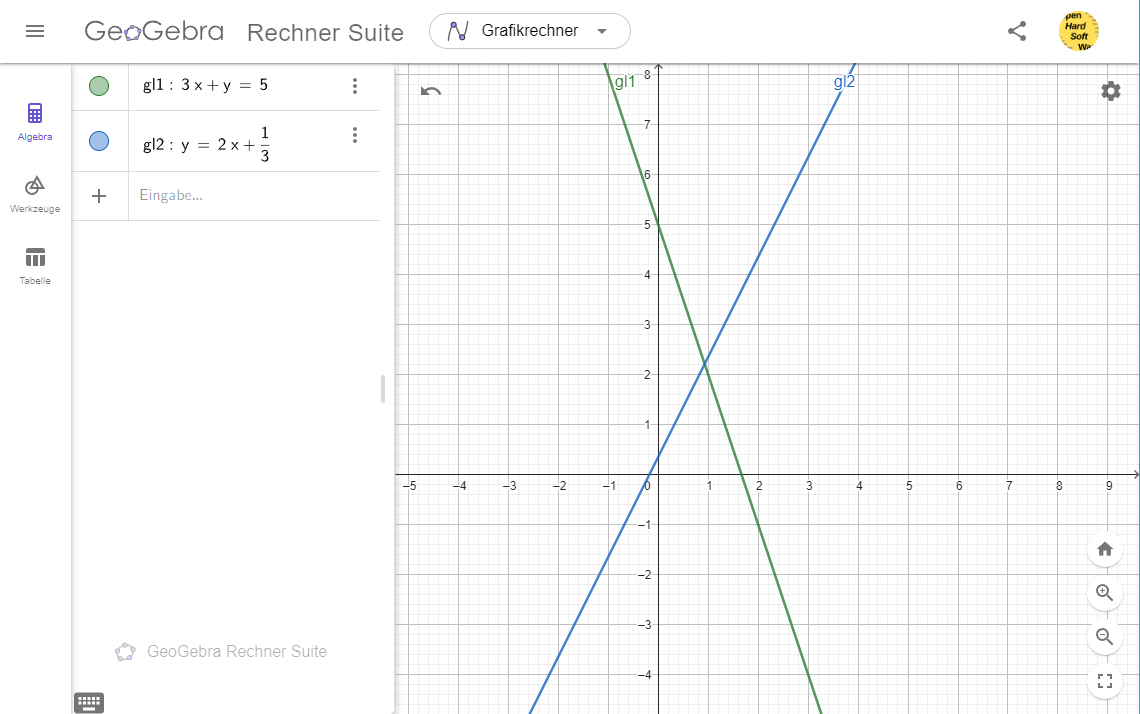
Aufgabe
Berechne $x_s$ und $y_s$ des gemeinsamen Schnittpunktes $\boxed{P_s=(x_s,y_s)}$
Lösung
Additionsverfahren
Gegebensei das folgende lineare Gleichungssystem:
$\boxed{2x + 3y = 4}$ (31)
$\boxed{3x + 4y = 5}$ (32)
Grafik
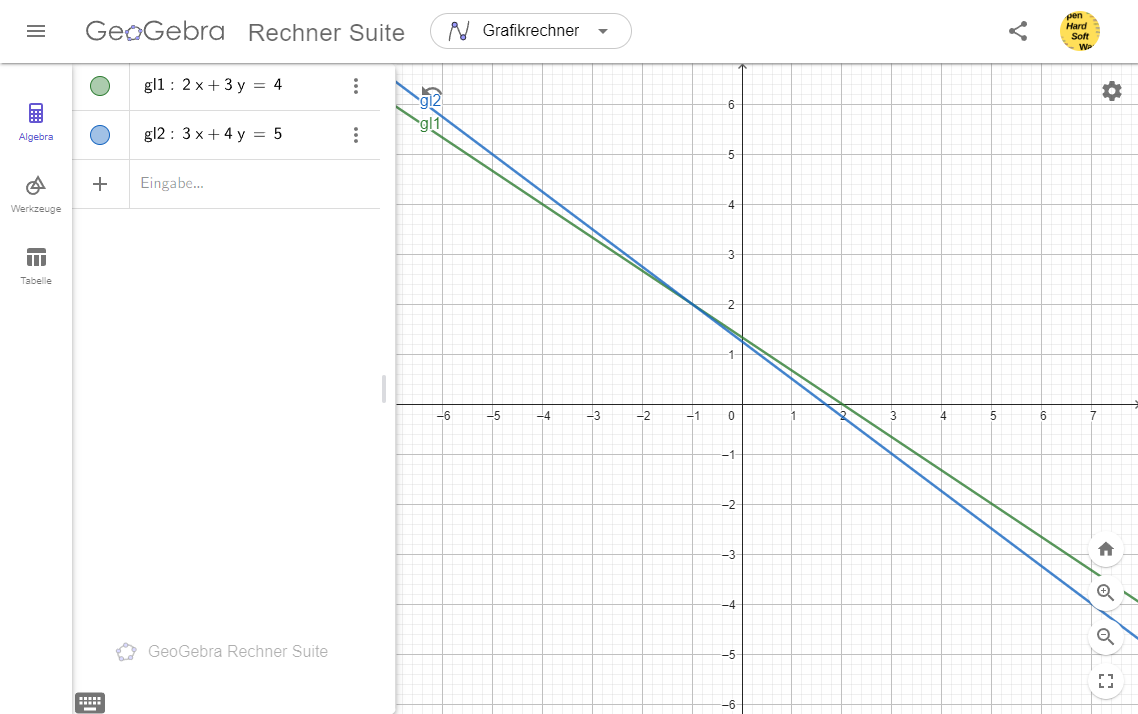
Aufgabe
Berechne $x_s$ und $y_s$ des gemeinsamen Schnittpunktes $\boxed{P_s=(x_s,y_s)}$
Lösung
Forme die Gleichungen so um, dass bei Addition oder Subtraktion der einen Gleichung
mit / von der anderen Gleichung eine Variable ($x$ oder $y$) wegfällt !
$2x + 3y = 4$ (*31)
$3x + 4y = 5$ (*32)
$6x + 9y = 12$
$3x + 4y = 5$
$6x + 9y = 12$ (33)
$6x + 8y = 10$ (34)
Subtrahiere (34) von (33):
$6x - 6x + 9y - 8y = 12 - 10$
$\boxed{y_s = 2}$ (35)
Einsetzen in (31) [oder (32)]:
$2x_s + 3[2] = 4$
$2x_s + 6 = 4$
$2x_s = -2$
$\boxed{x_s = -1}$ (36)
Mit dem Additionsverfahren bestimmt sich der Schnittpunkt:
$\boxed{P_s=(x_s,y_s) = (-1,2)}$ (37)
als Lösung des linearen Gleichungssystems:
$\boxed{2x + 3y = 4}$ (*31)
$\boxed{3x + 4y = 5}$ (*32)
Allgemeines Analytisches Verfahren
Gegebensei das folgende lineare Gleichungssystem:
$\boxed{ax + by ~= c~}$ (41) mit $a,b,c \in \mathbb{R}$
$\boxed{ux + vy = w}$ (42) mit $u,v,w \in \mathbb{R}$ und mit $x,y \in \mathbb{R}$
Bemerkungen
• Die Herleitung der hier angegeben Berechnungen findet ihr im Hauptkapitel:
"Lineare Gleichungssysteme"
• Die Gleichungen (41) und (42) können mit dem Gleichsetzungsverfahren
oder dem Einsetzungsverfahren oder dem Additionsverfahren gelöst werden.
• Vorteil einer allgemeinen Lösung, welche direkt in Computer-Programmen
zur Berechnung des Schnittpunktes zweier Geraden genutzt wird !
Aufgabe
Berechne $x_s$ und $y_s$ des gemeinsamen Schnittpunktes $\boxed{P_s=(x_s,y_s)}$ (43) beider Geraden.
Lösung
Mit dem Allgemeinem Analytischen Verfahren bestimmt sich der Schnittpunkt:
$\boxed{P_s=(x_s,y_s)}$ (43) mit $\boxed{x_s = \dfrac{cv - bw}{av - bu}}$ (44) und $\boxed{y_s = \dfrac{aw - cu}{av - bu}}$ (45)
als Lösung des linearen Gleichungssystems:
$\boxed{ax + by ~= c~~}$ (*41)
$\boxed{ux + vy ~= w}$ (*42)
Notwendige Bedingung für die Existenz exakt eines gemeinsamen Schnittpunktes $P_s$:
Nenner : $\boxed{av - bu \neq 0}$ (sonst Division durch Null !)
Bei dem Nenner : $\boxed{av - bu = 0}$ existiert kein Schnittpunkt, da beide Geraden parallel liegen !
Determinantenverfahren
Gegebensei das folgende lineare Gleichungssystem:
$\boxed{ax + by ~= c~}$ (51) mit $a,b,c \in \mathbb{R}$
$\boxed{ux + vy = w}$ (52) mit $u,v,w \in \mathbb{R}$ und mit $x,y \in \mathbb{R}$
Bemerkungen
• Auf die Herleitung der hier angegeben Berechnungen muss leider verzichtet werden!
• Vorteil einer allgemeinen Lösung, welche direkt in Computer-Programmen
zur Berechnung des Schnittpunktes zweier Geraden genutzt wird !
Aufgabe
Berechne $x_s$ und $y_s$ des gemeinsamen Schnittpunktes $\boxed{P_s=(x_s,y_s)}$ (53) beider Geraden.
Lösung
Die Lösung für $P_s=(x_s,y_s)$ lautet:
$\boxed{x_s = \dfrac{D_x}{D}}$ (54) und $\boxed{y_s = \dfrac{D_y}{D}}$ (55)
Mit den Zwischenberechnungen:
$\boxed{D_x := cv - bw}$ (56) und $\boxed{D_y := aw - cu}$ (57) und $\boxed{D := av - bu~~}$ (58)
Notwendige Bedingung für die Existenz exakt eines gemeinsamen Schnittpunktes $P_s$:
$\boxed{D = av - bu \neq 0}$ (sonst Division durch Null !)
Bei $\boxed{D = av - bu = 0}$ existiert kein Schnittpunkt, da beide Geraden parallel liegen !
Homepage WebSites Unterrichtsstunden Mathematik