Kapitel 1 : Lineare Gleichungssysteme
1.0 Überblick
1.1 Lösung linearer Gleichungssysteme
1.2 Lineare Gleichungen mit zwei Variablen
1.3 Lineare Gleichungssystem grafisch lösen
1.4 Lösen von linearen Gleichungssystemen ohne CAS
1.5 Lösen von linearen Gleichungssystemen mit CAS
1.6 Anwendungen
1.7 Einfache Aufgaben
1.8 Lösungsverfahren
Quellen
Lambacher Schweizer: "Mathematik für Gymnasien Klasse 9" [ISBN: 978-3-12-734291-8]Klett Verlag : Lambacher Schweizer Mathematik 9
1.4 Lösen von linearen Gleichungssystemen ohne CAS
Einführung in das Problem
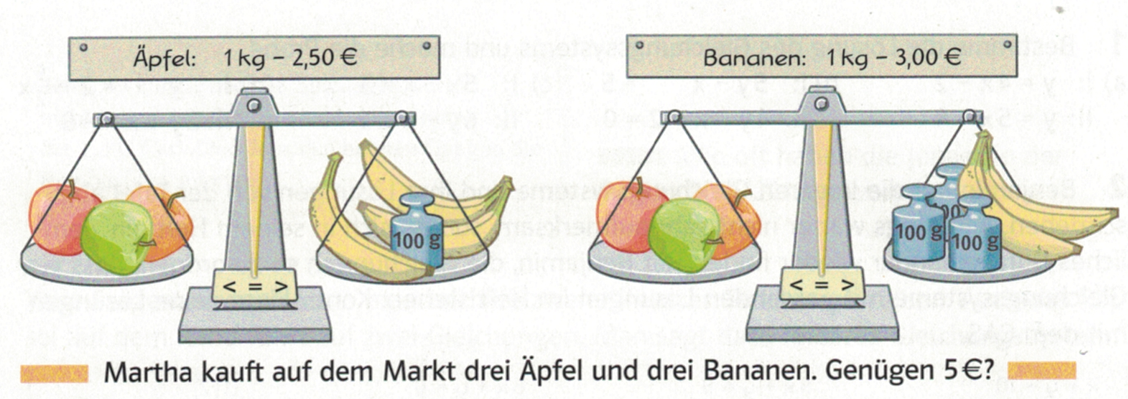
$\boxed{3G_a = 3G_b + 100g}$ (1): Drei Äpfel wiegen so viel wie drei Bananen plus 100g
$\boxed{3G_A = 2G_b + 300g}$ (2): Drei Äpfel wiegen so viel wie zwei Bananen plus 300g
Bestimme das (unbekannte) Gewicht der Äpfel $G_a$ und das (unbekannte) Gewicht der Birnen $G_b$
Berechnung:
$3G_a = 3G_b + 100g$ (1)
$3G_a = 2G_b + 300g ~~\big\vert~~$ Gleichung 2 von Gleichung 1 abziehen
$-------$
$0 = G_b - 200g \Rightarrow \boxed{G_b = 200g}$ (3)
$G_b=200$ in (1) einsetzen:
$3G_a = 3 \cdot 200g + 100g$
$G_a = 200g + \dfrac{100}{3}g$
$G_a = \dfrac{600}{3}g + \dfrac{100}{3}g$
$\boxed{G_a = \dfrac{700}{3}g}$ (4)
Bestimme die Gesamtkosten $K$ des Obsteinkaufs:
$\boxed{K = G_a \cdot \dfrac{2.5€}{1000g} + G_b \cdot \dfrac{3.0€}{1000g}}$ (5)
einsetzen (3) und (4) in (5):
$K = \dfrac{700}{3}g \cdot \dfrac{2.5€}{1000g} + 200g \cdot \dfrac{3.0€}{1000g}$
$K = \dfrac{700g}{3} \cdot \dfrac{2.5€}{1000g} + \dfrac{200g}{1} \cdot \dfrac{3.0€}{1000g}$
$K = \dfrac{700 \cdot 2.5}{3 \cdot 1000} \cdot \dfrac{€\cdot g}{g} + \dfrac{200 \cdot 3.0}{1 \cdot 1000} \cdot \dfrac{€ \cdot g}{g}$
$K = \dfrac{700 \cdot 2.5}{3 \cdot 1000} € + \dfrac{200 \cdot 9.0}{3 \cdot 1000} €$
$K = \dfrac{700 \cdot 2.5 + 200 \cdot 9.0}{3 \cdot 1000} €$
$K = \dfrac{1750 + 1800}{3000} €$
$K = \dfrac{3350}{3000} €$
$\boxed{K = 1.18 €}$ : Die Kosten des Einkaufs liegen (weit) unter dem zur Verfügung stehenden Betrag von $5€$ !
Lösung von Gleichungssystemen: Gleichsetzungsverfahren
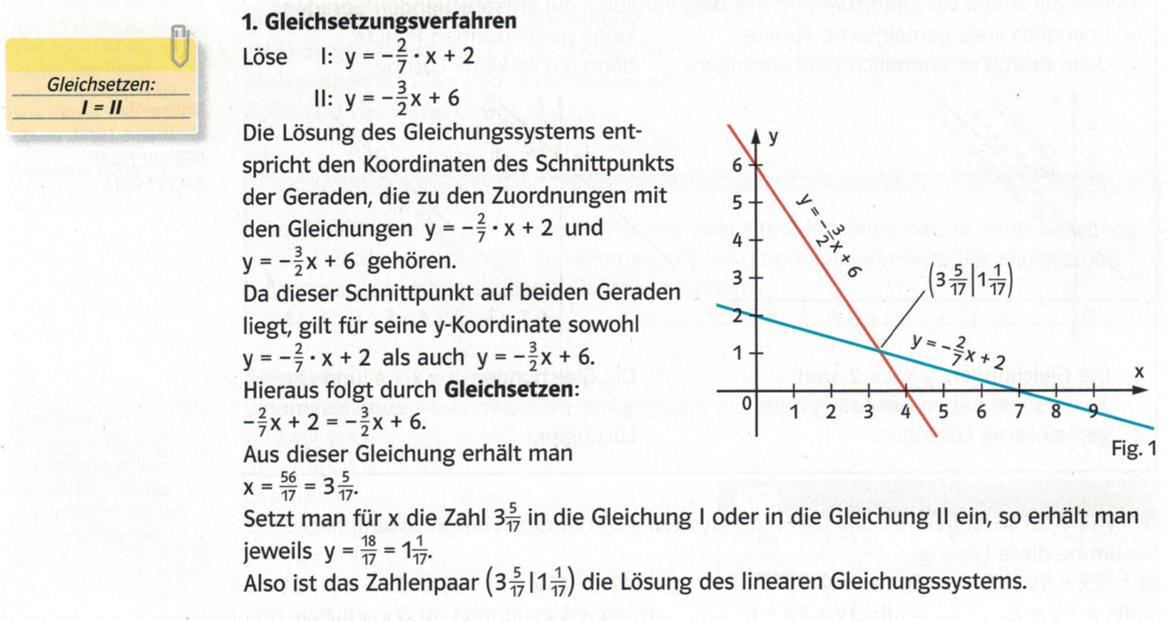
Lösung von Gleichungssystemen: Einsetzungsverfahren

Lösung von Gleichungssystemen: Additionsverfahren



Homepage WebSites Unterrichtsstunden Mathematik