Kapitel 1 : Lineare Gleichungssysteme

1.0 Überblick

1.1 Lösung linearer Gleichungssysteme

1.2 Lineare Gleichungen mit zwei Variablen

1.3 Lineare Gleichungssystem grafisch lösen

1.4 Lösen von linearen Gleichungssystemen ohne CAS

1.5 Lösen von linearen Gleichungssystemen mit CAS

1.6 Anwendungen

1.7 Einfache Aufgaben

1.8 Lösungsverfahren

Quellen

Lambacher Schweizer: "Mathematik für Gymnasien Klasse 9" [ISBN: 978-3-12-734291-8]
Klett Verlag : Lambacher Schweizer Mathematik 9

---

1.7 Einfache Aufgaben

---

Seite 20 - Wochenendrätsel

Problemdefinition

  •   In einer Obstschale befinden sich drei Birnen mehr als Äpfel:
      Anzahl Äpfel bezeichnen wir mit $x$
      Anzahl Birnen bezeichnen wir mit $y$
      $\Rightarrow \boxed{x + 3 = y}$   (1)
  •   Zieht man die Anzahl der Äpfel $x$ von der Zahl $5$ ab, so erhält man die Anzahl der Birnen $y$ :
      $\Rightarrow \boxed{5 - x = y}$   (2)

Aufgabe

  •   Bestimme die Zahl der Äpfel $x$ und die Zahl der Birnen $y$ !

Bemerkungen

  •   Der Definitionsbereich für $x$ und $y$ sind die Reellen Zahlen: $x \in \mathbb{R}$ und $y \in \mathbb{R}$
  •   Uns interessieren aber nur die Werte für $x$ und $y$ aus dem Bereich der Natürlichen Zahlen: $x \in \mathbb{N}$ und $y \in \mathbb{N}$
      $\rightarrow$ $x$ und $y$ müssen ganz und positiv sein! ("Es gibt keine negativen Äpfel !")
  •   Jede der beiden Gleichungen (1) und (2) hat unendlich viele Lösungen:
      wähle ich die Zahl $x = 3$ für $x$, so erhalte ich
      aus Gleichung (1) : $y = 6$
      aus Gleichung (2) : $y = 2$
      Mit der Zahl der Äpfel $x = 3$ kann ich also nicht eindeutig die Zahl der Birnen $y = 6$ bzw. $y = 2$ bestimmen:
      $\rightarrow$ die Gleichung (1) ergibt mit der Zahl der Äpfel $x = 3$ eine andere Birnenanzahl als die Gleichung (2) !
  •   Daher suchen wir DIE Zahl der Äpfel $x = ?$, mit welcher die Zahl der Birnen $y=?$ eindeutig bestimmt ist !

Grafische Lösung

Eingabe der Gleichungen (1) und (2) auf GeoGebra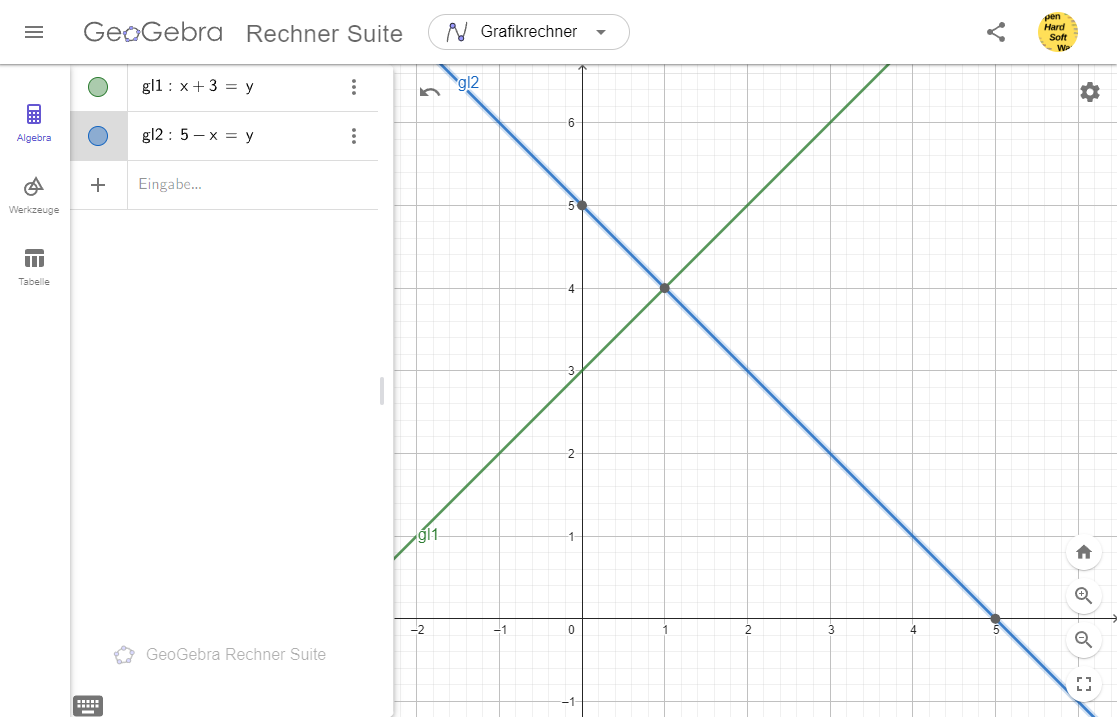


Ergebnis: wir sehen einen Schnittpunkt $P_s$ beider Geraden an den Stellen:
                $\boxed{P_s = (x_s,y_s) = (1,4)}$  (3)

Zur Probe setzen wir $x_s=1$ und $y_s=4$ in die Gleichungen (1) und (2) ein:
$x + 3 = y$   (*1)
$5 - x = y$   (*2)

Gleichung (1):
$x_s + 3 = y_s$
$1 + 3 = 4$   (q.e.d)

Gleichung (2):
$5 - x = y$
$5 - x_s = y_s$
$5 - 1 = 4$   (q.e.d)

$\Rightarrow$ Die Probe bestätigt die eindeutige Lösung $P_s = (x_s,y_s) = (1,4)$ (*3)
der Gleichungen   (*1) : $x + 3 = y$   und   (*2) : $5 - x = y$

Analytische Lösung

Ausgehend von den Gleichungen:
$x + 3 = y$   (*1)
$5 - x = y$   (*2)

versuchen wir $x$ aus beiden Gleichungen zu eleminieren:
$x_s + 3 = y_s$   (*1)
$\boxed{x_s = y_s - 3}$   (4)

Gleichung (4) einsetzen in (*2):
$5 - x_s = y_s$   (*2)
$5 - [y_s - 3] = y_s$

und erhalten dadurch eine Gleichung allein mit $y$
$5 - y_s + 3 = y_s$
$8 = 2y_s$
$y_s = \dfrac{8}{2}$
$\boxed{y_s = 4}$   (5)

Bestimmung von $x_s$ durch Einsetzung von $y_s=4$ in Gleichung (4):
$x_s = y_s - 3$   (*4)
$x_s = 4 - 3$
$\boxed{x_s = 1}$   (6)

Damit berechnen wir analytisch den Schnittpunkt : $P_s=(x_s,y_s)=(1,4)$
und erhalten ein Ergebnis identisch zum grafischen Schnittpunkt !

Antwort / Lösung

Als Antwort auf die Aufgabe: "Bestimme die Zahl der Äpfel $x$ und die Zahl der Birnen $y$" ergibt sich:
  •   Die Anzahl der Äpfel ist $\boxed{x = 1}$
  •   Die Anzahl der Birnen ist $\boxed{y = 4}$

---

Homepage    WebSites    Unterrichtsstunden    Mathematik