Kapitel 1 : Lineare Gleichungssysteme
1.0 Überblick
1.1 Lösung linearer Gleichungssysteme
1.2 Lineare Gleichungen mit zwei Variablen
1.3 Lineare Gleichungssystem grafisch lösen
1.4 Lösen von linearen Gleichungssystemen ohne CAS
1.5 Lösen von linearen Gleichungssystemen mit CAS
1.6 Anwendungen
1.7 Einfache Aufgaben
1.8 Lösungsverfahren
Quellen
Lambacher Schweizer: "Mathematik für Gymnasien Klasse 9" [ISBN: 978-3-12-734291-8]Klett Verlag : Lambacher Schweizer Mathematik 9
1.1 Lösung linearer Gleichungssysteme
1. Termwertberechnungen mit einem CAS
Anleitung zum Umgang mit einem CAS

Aufgabe zur Termberechnung mit einem CAS

2. Termumformungen mit einem CAS
Ausmultiplizieren mit einem CAS - "expand"

Ausklammern mit einem CAS - "factor"

3. Gleichungen lösen mit einem CAS

4. Was gehört zusammen?

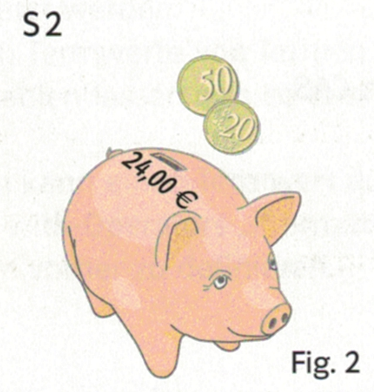
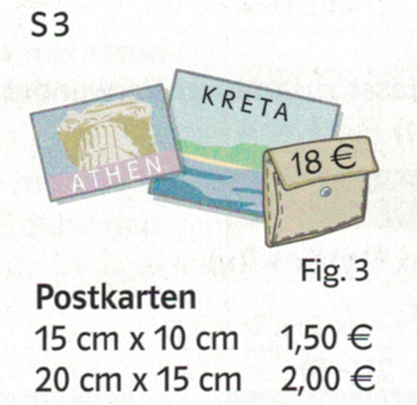

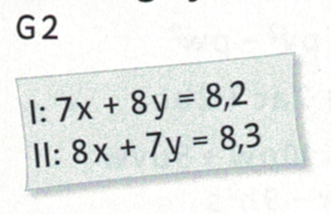
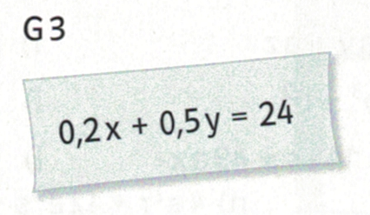
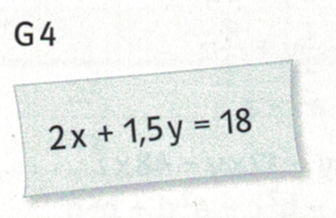
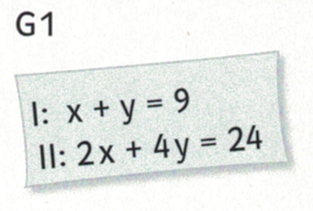
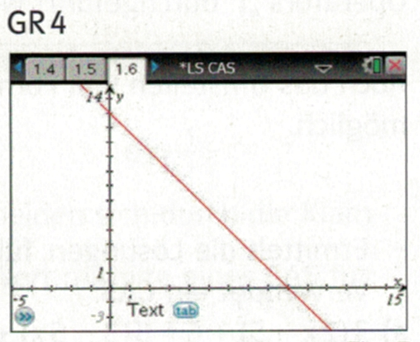
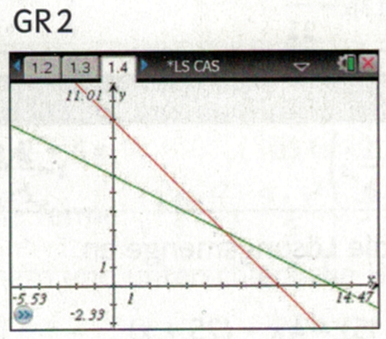
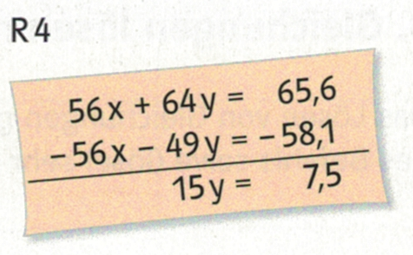
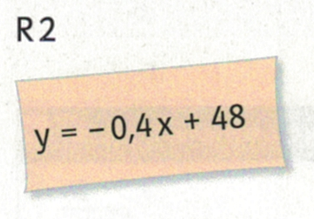
5. Mit Jena und Gotha in die 2. Bundesliga

Aufgabe: Spielekonsole

Aufgabe: nach wieviel Monaten $x$ haben M und A das gleiche Geld G angespart?
Lösung:
$G_M = 8x + 24$ und $G_A = 5x + 60$
Ansatz: $G_M = G_A$
$8x + 24 = 5x + 60$
$8x - 5x = 60 - 24$
$3x = 36$
$x = 12$
$\Rightarrow \boxed{x=12}$ Nach zwölf Monaten haben M und A das gleiche Geld gespart!
Aufgabe: Lösen einer Gleichung ohne CAS
Aufgabe: Löse die Gleichung (nach x auf): $\boxed{x(17 - 6x) - 5=(2x-1)(5-3x)}$ (1)$\Rightarrow 17x - 6x^2 - 5 = 2x(5-3x)-(5-3x)$
$17x - 6x^2 - 5 = 10x - 6x^2 - 5 + 3x$
$-6x^2 + 17x - 5 = -6x^2 + 3x + 10x - 5$
$17x = 3x + 10x$
$17x - 3x = 0$
$14x = 0 \Rightarrow$ Lösung: $x = 0$
Lösung: $\boxed{x = 0}$ (2) Lösungsmenge: $\boxed{L=\{0\}}$
Probe: (2) in (1) einsetzen:
$\boxed{x(17 - 6x) - 5=(2x-1)(5-3x)}~~\big\vert x = 0$
$0 \cdot (17 - 6 \cdot 0) - 5=(2 \cdot 0 -1)(5-3\cdot 0)$
$-5=(-1)(5-0)$
$-5=-5 ~~$ q.e.d. (wahre Aussage)
Aufgabe: Lösen einer Gleichung mit CAS - "solve"

Aufgabe: Lösen einer Ungleichung mit CAS - "solve"

Homepage WebSites Unterrichtsstunden Mathematik