Kapitel 1 : Lineare Gleichungssysteme
1.0 Überblick
1.1 Lösung linearer Gleichungssysteme
1.2 Lineare Gleichungen mit zwei Variablen
1.3 Lineare Gleichungssystem grafisch lösen
1.4 Lösen von linearen Gleichungssystemen ohne CAS
1.5 Lösen von linearen Gleichungssystemen mit CAS
1.6 Anwendungen
1.7 Einfache Aufgaben
1.8 Lösungsverfahren
Quellen
Lambacher Schweizer: "Mathematik für Gymnasien Klasse 9" [ISBN: 978-3-12-734291-8]Klett Verlag : Lambacher Schweizer Mathematik 9
1.2 Lineare Gleichungen mit zwei Variablen
Einführung: Gleichungen mit zwei Variablen
bisher: Gleichungen mit einer Variablen: $4x = 36$jetzt: Gleichungenen mit zwei Variablen: $4x + 6y = 36$

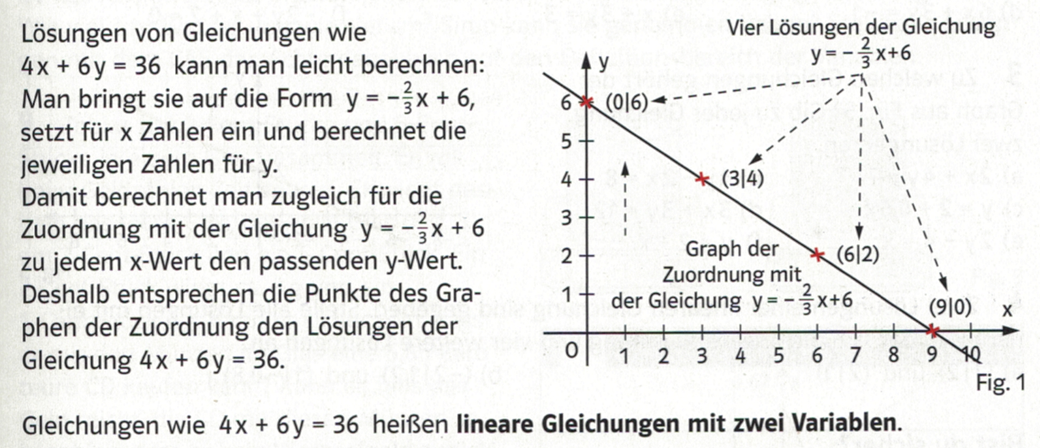
$4x + 6y = 36$ : linear in $x$ und $y$ da nur Potenzen $1$ vorhanden: $x^1$ und $y^1$
Bemerkung: Nullstelle der linearen Gleichung $4x + 6y = 36$
$4x_n + 6y_n = 36 ~~\big\vert~~y_n=0$
$4x_n + 6\cdot0 = 36$
$4x_n = 36$
$\boxed{x_n = 9}$
Bemerkung: Achsenabschnitt der linearen Gleichung $4x + 6y = 36$
$4x_a + 6y_a = 36 ~~\big\vert~~x_a=0$
$4 \cdot 0 + 6y_a = 36$
$6y_a = 36$
$\boxed{y_a = 6}$
WICHTIG: Lösungen der linearen Gleichung $4x + 6y = 36$

Gleichungen mit zwei Variablen in allgemeiner Form
Allgemeine lineare Gleichung mit zwei Variablen:$\boxed{ax + by = c}$
Nullstelle der allgemeinen linearen Gleichung:
$ax_n + by_n = c~~\big\vert~~y_n=0$
$ax_n + b \cdot 0 = c$
$ax_n = c$
$\boxed{x_n = \dfrac{c}{a}}$
Achsenabschnitt der allgemeinen linearen Gleichung:
$ax_a + by_a = c~~\big\vert~~x_a=0$
$a \cdot 0 + by_a = c$
$by_a = c$
$\boxed{y_a = \dfrac{c}{b}}$
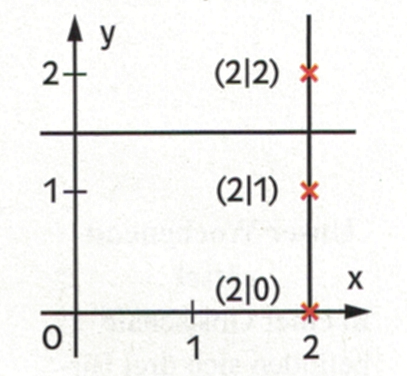
Sonderfälle für Gleichungen mit zwei Variablen

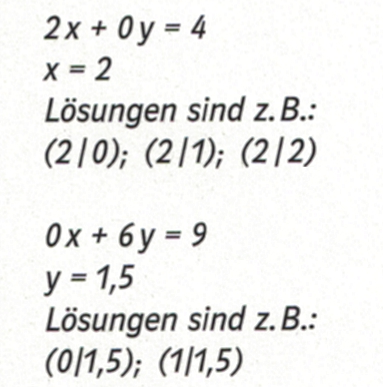
Homepage WebSites Unterrichtsstunden Mathematik