Kapitel 1 : Lineare Gleichungssysteme
1.0 Überblick
1.1 Lösung linearer Gleichungssysteme
1.2 Lineare Gleichungen mit zwei Variablen
1.3 Lineare Gleichungssystem grafisch lösen
1.4 Lösen von linearen Gleichungssystemen ohne CAS
1.5 Lösen von linearen Gleichungssystemen mit CAS
1.6 Anwendungen
1.7 Einfache Aufgaben
1.8 Lösungsverfahren
Quellen
Lambacher Schweizer: "Mathematik für Gymnasien Klasse 9" [ISBN: 978-3-12-734291-8]Klett Verlag : Lambacher Schweizer Mathematik 9
Überblick : Lineare Gleichungssysteme
Was sind Lineare Gleichungssysteme?
Gegeben sind zwei lineare Gleichungen mit den Unbekannten $x$ und $y$ :$\boxed{x + y = 9}$ (1)
$\boxed{2x + 4y = 24}$ (2)
Linear sind die Gleichungen wegen der Potenzen $1$ bei $x$ und $y$ :
$x = 1 \cdot x^1$
$4y = 4 \cdot y^1$
Gesucht:
sind nun die Werte für $x$ und $y$ aus der Menge der Reellen Zahlen,
welche die beiden Gleichungen (1) und (2) zugleich erfüllen!
Grafische Darstellung linearer Gleichungssysteme
Umformung der Gleichungen (1) und (2) nach $y$ :
(*1) : $x + y = 9$ $~~\big\vert ~-x$
$x + y - x = 9 - x$
$y = 9 - x$
$\boxed{y = -x + 9}$ (3)
Gleichung (3) ist eine äquivalente Darstellung zu Gleichung (1) !
(*2) : $2x + 4y = 24$ $~~\big\vert ~-2x$
$2x + 4y - 2x = 24 - 2x$
$4y = 24 - 2x$
$4y = -2x + 24$ $~~\big\vert ~/4$
$y = -\dfrac{2x}{4} + \dfrac{24}{4}$
$\boxed{y = -\dfrac{1}{2}x + 6}$ (4)
Gleichung (4) ist eine äquivalente Darstellung zu Gleichung (2) !
Nebenrechnung:
• Nullstelle der Gleichung (1)(3) : $y = -x + 9$
Setze $y_n = 0$ $~~\Rightarrow~~$ $0 = -x_n + 9$
$\boxed{x_n = 9}$ (5)
• Nullstelle der Gleichung (2)(4) : $y = -\dfrac{1}{2}x + 6$
Setze $y_n = 0$ $~~\Rightarrow~~$ $0 = -\dfrac{1}{2}x_n + 6$
$0 = \dfrac{1}{2}x_n - 6$
$0 = x_n - 12$
$\boxed{x_n = 12}$ (6)
Interpretation der Darstellung
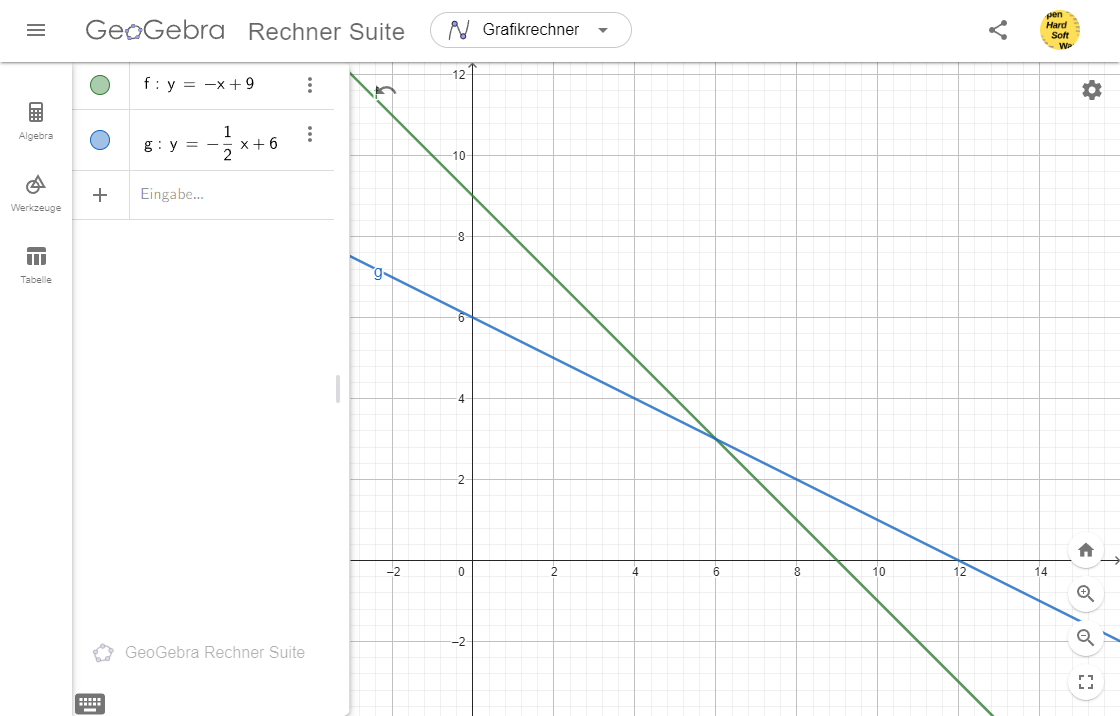
• Die Gleichung (1)(3) : $y = -x + 9$ hat die Steigung $-1$ und den Achsenabschnitt $9$ (und die Nullstelle $9$)
• Die Gleichung (2)(4) : $y = -\dfrac{1}{2}x + 6$ hat die Steigung $-\dfrac{1}{2}$ und den Achsenabschnitt $6$ (und die Nullstelle $12$)
• Wir sehen den einzigen Schnittpunkt der beiden Geraden: $\boxed{S = (x_s, y_s) = (6, 3)}$ (7)
• Setzen wir diesen Schnittpunkt $S$ in die Gleichungen (1)(3) und (2)(4) ein:
$x + y = 9$ (*1)
$x_s + y_s = 9$ $~~\big\vert ~x_s = 6 ~~~~y_s = 3$
$6 + 3 = 9 ~~~\Rightarrow$ Schnittpunkt $S = (x_s, y_s) = (6, 3)$ erfüllt die Gleichung (1) und damit auch (3)
$2x + 4y = 24$ (*2)
$2x_s + 4y_s = 24$ $~~\big\vert ~x_s = 6 ~~~~y_s = 3$
$2 \cdot 6 + 4 \cdot 3 = 24$
$12 + 12 = 24 ~~~\Rightarrow$ Schnittpunkt $S = (x_s, y_s) = (6, 3)$ erfüllt die Gleichung (2) und damit auch (4)
Damit bildet $\boxed{S = (x_s, y_s) = (6, 3)}$ (*7) die Lösung des
linearen Gleichungssystems: $\boxed{x + y = 9}$ (*1) und $\boxed{2x + 4y = 24}$ (*2)
• Bemerkung zur Lösung:
• In unserem Fall existiert genau EIN Schnittpunkt beider Geraden-Gleichungen, da die Geraden
NICHT PARALLEL verlaufen!
• Für den Fall PARALLEL verlaufender Geraden gibt es KEINEN Schnittpunkt und damit
KEINE Lösung des linearen Gleichungssystems!
Analytische Lösung des gemeinsamen Schnittpunktes beider Geraden (1) und (2)
Gegeben : sind die beiden linearen Gleichungen mit den Unbekannten $x$ und $y$ (siehe oben):
$x + y = 9$ (*1)
$2x + 4y = 24$ (*2)
Gesucht : sind der Wert für $x_s = ?$ und der Wert für $y_s = ?$, welcher beide Gleichungen (*1) und (*2) erfüllt (grafisch: gemeinsamer Schnittpunkt!)
Spezielle analytische Lösung zur Berechnung des Schnittpunktes beider Geraden (1) und (2):
• Setze $\boxed{x = x_s}$ und $\boxed{y = y_s}$ in beiden Gleichungen (*1) und (*2):
$x_s + y_s = 9$ (11)
$2x_s + 4y_s = 24$ (12)
Wir erhalten zwei Geraden-Gleichungen mit zwei Unbekannten $x_s$ und $y_s$,
welche den gemeinsamen Schnittpunkt $P_s = (x_s,y_s)$ bilden.
Wir versuchen nun, aus beiden Gleichungen eine Gleichung mit einer Unbekannten zu erhalten:
• Bestimme $x_s$ :
Löse Gleichung (*11) nach $y_s$ auf:
$y_s = 9 - x_s$
Einsetzen in (12) ergibt:
$2x_s + 4y_s = 24$
$2x_s + 4(9 - x_s) = 24$
Auflösen nach $x_s$ :
$-2x_s = -12$
$\boxed{x_s = 6}$ (13)
Damit stimmt der X-Wert des grafisch ermittelten Schnittpunktes
$P_{s(grafisch)} = (6, 3)$ mit dem analytisch errechneten Wert überein!
• Bestimme $y_s$ :
Gleichung (*11) ergibt mit $x_s = 6$ :
$x_s + y_s = 9$ (*11)
$6 + y_s = 9$
Auflösen nach $y_s$ :
$y_s = 9 - 6$
$\boxed{y_s = 3}$ (14)
Auch der berechnete Y-Wert des Schnittpunktes stimmt mit dem grafischen Schnittpunkt überein!
• Damit ergibt sich der Schnittpunkt beider Geraden mit:
$\boxed{P_s = (x_s, y_s)= (6, 3)}$ (15)
Verallgemeinerung: Analytische Lösung des gemeinsamen Schnittpunktes zweier Geraden
Gegeben:
• zwei Geradengleichungen:
$\boxed{ax + by = c}$ (31) mit gegebenen $a,b,c \in \mathbb{R}$ und $x,y \in \mathbb{R}$
$\boxed{ux + vy = w}$ (32) mit gegebenen $u,v,w \in \mathbb{R}$
Gesucht:
• der gemeinsame Schnittpunkt $P_s$ beider Geraden (31) und (32) mit:
$\boxed{P_s = (x_s,y_s)}$ (33) mit $x_s,y_s \in \mathbb{R}$
Die Aufgabe besteht darin, $x_s$ und $y_s$ eindeutig als Schnittpunkt $P_s$
beider Geraden (31) und (32) zu bestimmen!
Herleitung:
• Die Gleichungen (31) und (32) mit jeweils den Unbekannten $x$ und $y$
werden auf zwei Gleichungen für $x_s = ...$ und $y_s = ...$ reduziert. Damit müssen $x_s$ und $y_s$ beide Gleichungen erfüllen!
• $x=x_s$ und $y=y_s$ in Gleichung (31) und (32) einsetzen:
$ax + by = c$ (*31)
$ux + vy = w$ (*32)
$ax_s + by_s = c$ (34)
$ux_s + vy_s = w$ (35)
• Gleichung (34) nach $y_s$ auflösen:
$ax_s + by_s = c$ (*34)
$by_s = -ax_s + c$
$\boxed{y_s = -\dfrac{a}{b}x_s + \dfrac{c}{b}}$ (36)
• Gleichung (36) in Gleichung (35) einsetzen (Elemination $y_s$):
$ux_s + vy_s = w$ (*35)
$ux_s + v[-\dfrac{a}{b}x_s + \dfrac{c}{b}] = w$
$bux_s + v[-ax_s + c] = bw$
$bux_s - avx_s + cv = bw$
$x_s[bu - av] + cv = bw$
$x_s[bu - av] = bw - cv$
$x_s = \dfrac{bw - cv}{bu - av}$
$\boxed{x_s = \dfrac{cv - bw}{av - bu}}$ (37)
• Gleichung (37) in (36) einsetzen (Elemination $x_s$):
$y_s = -\dfrac{a}{b}x_s + \dfrac{c}{b}$ (*36)
$y_s = \dfrac{c - a x_s}{b}$
$y_s = \dfrac{c - a [\dfrac{bw - cv}{bu - av}]}{b}$
$y_s = \dfrac{c}{b} - \dfrac{a}{b} \cdot \dfrac{bw - cv}{bu - av}$
$y_s = \dfrac{c}{b} - \dfrac{a(bw - cv)}{b(bu - av)}$
$y_s = \dfrac{c(bu - av)}{b(bu - av)} - \dfrac{a(bw - cv)}{b(bu - av)}$
$y_s = \dfrac{c(bu - av) - a(bw - cv)}{b(bu - av)}$
$y_s = \dfrac{(bcu - acv) - (abw - acv)}{b(bu - av)}$
$y_s = \dfrac{bcu - acv - abw + acv}{b(bu - av)}$
$y_s = \dfrac{b(cu - aw)}{b(bu - av)}$
$y_s = \dfrac{cu - aw}{bu - av}$
$\boxed{y_s = \dfrac{aw - cu}{av - bu}}$ (38)
Probe:
• Lösungsgleichungen (37) und (38) in Ausgangsgleichungen (31) und (32) einsetzen:
$x_s = \dfrac{bw - cv}{bu - av}$ (*37)
$y_s = \dfrac{aw - cu}{av - bu}$ (*38)
$ax + by = c$ (*31)
$ux + vy = w$ (*32)
• Probe mit Gleichung (34) :
$ax_s + by_s = c$ (*34)
$a\dfrac{bw - cv}{bu - av} + b\dfrac{aw - cu}{av - bu} = c$
$a(bw - cv)(av - bu) + b(aw - cu)(bu - av) = c(bu - av)(av - bu)$
$(abw - acv)(av - bu) + (abw - bcu)(bu - av) = (bcu - acv)(av - bu)$
$\overline{aabvw} \overline{- aacvv} \overline{- abbuw} \overline{+ abcuv} \overline{+ abbuw} \overline{- bbcuu} \overline{- aabvw} \overline{+ abcuv} = $
$= \overline{abcuv} \overline{- aacvv} \overline{- bbcuu} \overline{+ abcuv}$ (q.e.d)
Damit lösen die Gleichungen (37) für $x_s$ und (38) für $y_s$ die Geradengleichung (31) .
• Probe mit Gleichung (35) :
$ux_s + vy_s = w$ (*35)
$u\dfrac{bw - cv}{bu - av} + v\dfrac{aw - cu}{av - bu} = w$
$\dfrac{buw - cuv}{bu - av} + \dfrac{avw - cuv}{av - bu} = w$
$\dfrac{buw - cuv}{bu - av}(bu - av)(av - bu) + \dfrac{avw - cuv}{av - bu}(av - bu)(bu - av) = w(bu - av)(av - bu)$
$(buw - cuv)(av - bu) + (avw - cuv)(bu - av) = (buw - avw)(av - bu)$
$(abuvw - acuvv - bbuuw + bcuuv) + (abuvw - bcuuv - aavvw + acuvv)=$
$= abuvw - aavvw - bbuuw + abuvw$
$\overline{abuvw} \overline{- acuvv} \overline{- bbuuw} \overline{+ bcuuv} \overline{+ abuvw} \overline{- bcuuv} \overline{- aavvw} \overline{+ acuvv}=$
$= \overline{abuvw} \overline{- aavvw} \overline{- bbuuw} \overline{+ abuvw}$ (q..e.d)
Damit lösen die Gleichungen (37) für $x_s$ und (38) für $y_s$ die Geradengleichung (32) .
Ergebnis der Verallgemeinerung: Analytische Lösung des gemeinsamen Schnittpunktes zweier Geraden
Die Geradengleichungen (31) und (32) bei bekannten $a,b,c,u,v,w$ und unbekannten $x,y$:
$\boxed{ax + by = c}$ (31)
$\boxed{ux + vy = w}$ (32)
besitzen genau eine Lösung:
$\boxed{x_s = \dfrac{cv - bw}{av - bu}}$ (37)
$\boxed{y_s = \dfrac{aw - cu}{av - bu}}$ (38)
Fallunterscheidung
• Nenner ungleich Null: $\boxed{av - bu \neq 0}$ (39)
Es gibt genau eine Lösung $P_s=(x_s,y_s)$ im Schnittpunkt beider Geraden.
Daher verlaufen die Geraden NICHT parallel zueinander.
Die Berechnung von $P_s=(x_s,y_s)$ erfolgt über (37) und (38).
• Nenner gleich Null: $\boxed{av - bu = 0}$ (40)
Unterfall: Beide Geraden verlaufen parallel, liegen aber nicht aufeinander.
Es gibt KEINE Lösung und damit KEINEN Schnittpunkt.
(Division durch Null in (37) und (38) nicht erlaubt!)
Beispiel: $ax + by = c$ und $ux + vy = w$ mit $a=u, b=v, c \neq w$
Unterfall: Beide Geraden liegen aufeinander und verlaufen daher parallel.
Es gibt UNENDLICH VIELE Lösungen und damit UNENDLICH VIELE Schnittpunkte.
(Division durch Null in (37) und (38) nicht erlaubt!)
Beispiel: $ax + by = c$ und $ux + vy = w$ mit $a=u, b=v, c = w$
Vorteil der verallgemeinerten analytischen Lösung:
ALLE MÖGLICHEN AUFGABEN zum Schnittpunkt zweier Geraden entsprechend der Gleichungen (31) und (32) müssen nicht mehr mühselig von Hand durchgerechnet werden, sondern aus den Lösungsgleichungen (37) und (38) lässt sich direkt DIE EINZIGE LÖSUNG $P_s=(x_s,y_s)$ unter der Bedingung (39) berechnen!
Homepage WebSites Unterrichtsstunden Mathematik