Kapitel 1 : Teilbarkeit
1.1 Teiler und Vielfache
1.2 Teilbarkeitsregeln
1.3 Primzahlen, GGT und KGV
Quellen
Lambacher Schweizer: "Mathematik für Gymnasien Klasse 6" [ISBN: 978-3-12-733267-4]Klett Verlag : Lambacher Schweizer Mathematik 6
Wikipedia : Primzahl
Wikipedia : Sieb des Eratosthenes
Wikipedia : GGT - Grösster Gemeinsamer Teiler
Wikipedia : KGV - Kleinstes Gemeinsames Vielfaches
1.3 Primzahlen, GGT und KGV
Was ist eine Primzahl?
Definition:"Eine Primzahl ist eine natürliche Zahl, die grösser als $1$ ist und nur durch $1$ und sich selbst teilbar ist."
Folgerung:
"Eine Primzahl hat nur zwei Faktoren: $1$ und sich selbst."
Beispiel:
Die Primzahlen als Teilmenge der Natürlichen Zahlen (Mengensymbol: $\mathbb{N}$ ) zwischen $1$ und $100$ sind:
Primzahlen$[1 .. 100] = \{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97\}$
Schlussfolgerungen aus ihrer Definition:
• Existenz und Eindeutigkeit der Primfaktorzerlegung:
Jede natürliche Zahl grösser als $1$ kann als Produkt von einer oder mehreren Primzahlen geschrieben werden.
• Fundamentalsatz der Arithmetik:
Jede ganze Zahl grösser als $1$ kann eindeutig in ein Produkt von Primzahlen zerlegt werden.
• Sieb des Eratosthenes:
Algorithmus zum Auffinden aller Primzahlen in einem Zahlenbereich.
Primfaktorzerlegung
Wie erkennt man eine Primzahl?
Aufgabe: Ist die Zahl $z$ eine Primzahl?Vorgehensweise:
Bilde den ganzzahligen Rest $w$ der Wurzel aus $z$ : $w = int(\sqrt{z})$
Notiere die Menge $P = \{2, 3, .. w\}$ der Primzahlen von $2$ bis zu dieser Zahl $w$.
Mit der Menge der Primzahlen $P$ prüfen, ob diese $z$ ohne Rest teilen.
Teilt keine der Primzahlen aus $P$ $z$ ohne Rest, handelt es sich bei $z$ um eine Primzahl.
Sieb des Eratosthenes
Das Sieb des Eratosthenes ist ein Algorithmus zur Bestimmung einer Menge aller Primzahlen kleiner oder gleich einer vorgegebenen Zahl. Es ist nach dem griechischen Mathematiker Eratosthenes benannt.Sieb-Verfahren Wikipedia

Gegeben ist eine Tabelle mit den natürlichen Zahlen $M = \{2,3,4,5,..,120\} \in \mathbb{N}$ .
Registrierung aller Zahlen (von klein nach gross) $p$ als Primzahlen $p \in P = \{2,3,5,7,11,13,..,113\}$, welche noch nicht markiert sind und Markierung der Vielfachen dieser Zahlen als Vielfache (und nicht als Primzahlen).
Ergebnis der Primzahl-Siebung:
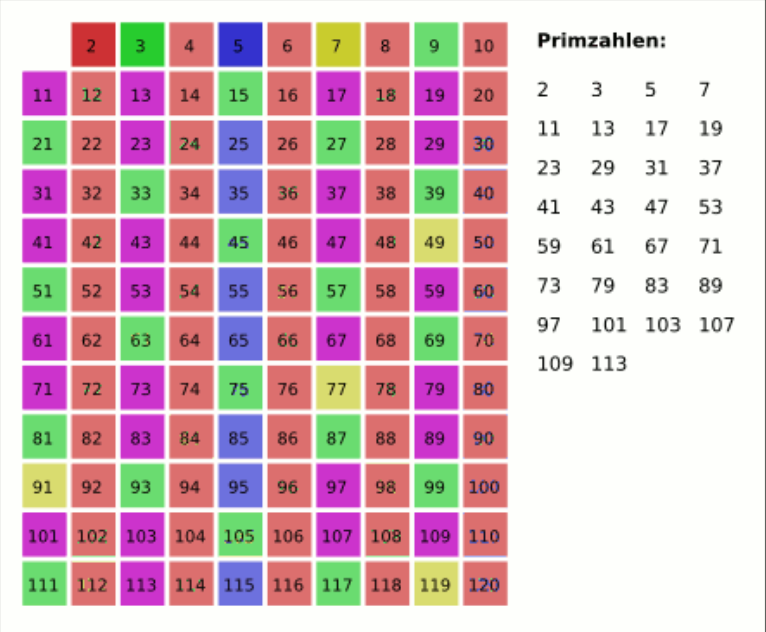
Sieb-Verfahren Lambacher Schweizer
Lambacher Schweitzer Klasse 6, 3 Primzahlen Seite 17:
Primzahl-Bestimmung $P = \{2,3,5,7,11,..,89,97\}$ für den Bereich $M = \{2,3,4,5,6,..,99,100\}$
GGT : Grösster Gemeinsamer Teiler
Primfaktorzerlegung : GGT
Definition:"Der GGT zweier ganzer Zahlen $a$ und $b$ ist die grösste natürliche Zahl,
durch die sich beide Zahlen ohne Rest teilen lassen."
Der grösste gemeinsame Teiler (GGT) zweier Zahlen $a$ und $b$ kann durch Primfaktorzerlegung bestimmt werden.
Hierbei werden zunächst die zwei Ausgangszahlen jeweils in ein Produkt kleiner Primzahlen
$a$ mit $p_i$ : $a = p_1 \cdot p_2 \cdot .. \cdot p_n \Rightarrow P=\{p_1,p_2, .. ,p_n\}$ und
$b$ mit $q_i$ : $b = q_1 \cdot q_2 \cdot .. \cdot q_m \Rightarrow Q=\{q_1,q_2, .. ,q_m\}$
zerlegt, welche als Primfaktoren $p_i$ und $q_i$ bezeichnet werden.
Bestimmt wird nun die Schnittmenge $S$ beider Mengen $P$ und $Q$:
$S = P \cap Q = \{s_1,s_2,..s_k\}$
mit den gemeinsamen Primfaktoren beider Zahlen $a$ und $b$.
Das GGT berechnet sich dann als Produkt aller Elemente der Schnittmenge $S$:
$\boxed{GGT = s_1 \cdot s_2 \cdot .. \cdot s_k}$
Beispiel: Bestimme den GGT von $1980$ und $840$
Lösung:
$~~~~~~~~~~~~~~~~~~~~1980 = 2 \cdot 2 ~~~~~\cdot 3 \cdot 3 \cdot 5 ~~~~~\cdot 11$
$~~~~~~~~~~~~~~~~~~~~~~840 = 2 \cdot 2 \cdot 2 \cdot 3 ~~~~~\cdot 5 \cdot 7$
$GGT(1980,840) = 2 \cdot 2 ~~~~~\cdot 3 ~~~~~\cdot 5$
$\boxed{GGT(1980,840) = 60}$
Euklidischer Algorithmus : GGT
Der Euklidische Algorithmus ist ein Verfahren zur Bestimmung des grössten gemeinsamen Teilers (GGT) zweier Zahlen. Er ist nach dem griechischen Mathematiker Euklid benannt, der ihn in seinem Werk “Die Elemente” beschrieben hat. Der Euklidische Algorithmus ist die schnellste Methode zur Berechnung des GGT.Euklidischer Algorithmus(1. Version: Differenz) : GGT
Beispiel: Bestimme den GGT von 840 und 1980
Lösung:
• Subtrahiere die kleine Zahl ($840$) von der grossen Zahl ($1980$) :
$1980 - 840 = 1140$
$1140 - 840 = 300$
$300 - 840 < 0 \Rightarrow$
• solange dieses möglich ist, sonst Subtrahend minus Differenz:
$840 - 300 = 540$
$540 - 300 = 240$
$240 - 300 < 0 \Rightarrow$
$300 - 240 = 60$
$60 - 240 < 0 \Rightarrow$
$240 - 60 = 180$
$180 - 60 = 120$
$120 - 60 = 60$
$60 = 60$
Der gesuchte GGT von $840$ und $1980$ ist $60$:
$\boxed{GGT(840,1980) = 60}$
Beispiel: Bestimme den GGT von 270 und 192
Lösung:
• Subtrahiere die kleine Zahl ($192$) von der grossen Zahl ($270$) :
$270 - 192 = 78$
$78 - 192 < 0 \Rightarrow$
$192 - 78 = 114$
$114 - 78 = 36$
$36 - 78 < 0 \Rightarrow$
$78 - 36 = 42$
$42 - 36 = 6$
$6 - 36 < 0 \Rightarrow$
$36 - 6 = 30$
$30 - 6 = 24$
$24 - 6 = 18$
$18 - 6 = 12$
$12 - 6 = 6$
$6 = 6$
Der gesuchte GGT von $270$ und $192$ ist $6$:
$\boxed{GGT(270,192) = 6}$
Euklidischer Algorithmus(2. Version: Quotient) : GGT
Beispiel: Bestimme den GGT von 270 und 192
Lösung:
• Teile die grosse Zahl ($270$) durch die kleine Zahl ($192$):
$270 : 192 = 1~R~78 \Rightarrow R \neq 0 \Rightarrow$
$192 : 78 = 2~R~36 \Rightarrow R \neq 0 \Rightarrow$
$78 : 36 = 2~R~6 \Rightarrow R \neq 0 \Rightarrow$
$36 : 6 = 6~R~0 \Rightarrow R = 0 \Rightarrow$
Der gesuchte GGT von $270$ und $192$ ist $6$:
$\boxed{GGT(270,192) = 6}$
KGV : Kleinstes Gemeinsames Vielfaches
Definition:"Das kleinste gemeinsame Vielfache KGV zweier ganzer Zahlen $a$ und $b$ ist die kleinste
positive natürliche Zahl, die sowohl Vielfaches von $a$ als auch Vielfaches von $b$ ist."
Vielfachen-Algorithmus : Bestimme KGV zweier Zahlen
Beispiel: Bestimme das KGV von 12 und 18Lösung:
• Die positiven Vielfachen von $12$ sind: $\{12,24,36,48,60,72,84,96,108,..\}$
• Die positiven Vielfachen von $18$ sind: $\{18,36,54,72,90,108,..\}$
• Die gemeinsamen Vielfachen von $12$ und $18$ sind: $\{36,72,108,..\}$
• Damit ist das kleinste gemeinsame Vielfache (KGV) von $12$ und $18$:
$\boxed{KGV(12,18) = 36}$
Primfaktor-Algorithmus : Bestimme KGV zweier Zahlen
Der kleinste gemeinsame Vielfache (KGV) zweier Zahlen $a$ und $b$ kann durch Primfaktorzerlegung bestimmt werden.Hierbei werden zunächst für die zwei Ausgangszahlen $a$ und $b$ in ein Produkt kleinster Primzahlen
$a$ mit $p_i$ : $a = p_1 \cdot p_2 \cdot .. \cdot p_n \Rightarrow P=\{p_1,p_2, .. ,p_n\}$ und
$b$ mit $q_i$ : $b = q_1 \cdot q_2 \cdot .. \cdot q_m \Rightarrow Q=\{q_1,q_2, .. ,q_m\}$
zerlegt, welche als Primfaktoren $p_i$ und $q_i$ bezeichnet werden. Die $p_i$ und $q_i$ dürfen auch mehrfach vorkommen.
Bestimmt wird nun die Vereinigungsmenge $V$ beider Mengen $P$ und $Q$:
$V = P \cap Q = \{s_1,s_2,..s_k\}$
mit allen Primfaktoren der Zahl $a$ und allen Primfaktoren der Zahl $b$.
Das KGV berechnet sich dann als Produkt aller Elemente der Vereinigungsmenge $V$:
$\boxed{KGV = s_1 \cdot s_2 \cdot .. \cdot s_k}$
Beispiel: Berechne das KGV von $72$ und $120$
Lösung:
$~~~~~~~~~~~~~~~~~~~~~72 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3$
$~~~~~~~~~~~~~~~~~~~120 = 2 \cdot 2 \cdot 2 \cdot 3 ~~~~~\cdot 5$
$KGV(72,120) = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 5 = 360$
$\boxed{KGV(72,120) = 360}$
Erweiterter Euklidischer Algorithmus : Bestimme KGV zweier Zahlen
Satz:"Das Produkt aus GGT und KGV zweier positiver Zahlen $a$ und $b$ ist gleich dem Produkt derselben Zahlen $a$ und $b$"
$\boxed{GGT(a,b) \cdot KGV(a,b) = a \cdot b}$
Folgerung:
Wenn also der $GGT(a,b)$ bekannt ist (beispielsweise durch den Euklidischen Algorithmus berechnet), so folgt für das $KGV(a,b)$ :
$\boxed{KGV(a,b) = \dfrac{a \cdot b}{GGT(a,b)}}$
Beispiel: Bestimme den KGV von 270 und 192.
Lösung:
• Bestimme den GGT mit dem Euklidischen Algorithmus:
Teile die grosse Zahl ($270$) durch die kleine Zahl ($192$):
$270 : 192 = 1~R~78 \Rightarrow R \neq 0 \Rightarrow$
$192 : 78 = 2~R~36 \Rightarrow R \neq 0 \Rightarrow$
$78 : 36 = 2~R~6 \Rightarrow R \neq 0 \Rightarrow$
$36 : 6 = 6~R~0 \Rightarrow R = 0 \Rightarrow$
Der gesuchte GGT von $270$ und $192$ ist $6$:
$\boxed{GGT(270,192) = 6}$
• $KGV(270,192) = \dfrac{270 \cdot 192}{GGT(270,192)} = \dfrac{51840}{6}$
• $\boxed{KGV(a,b) = 8640}$
Homepage WebSites Unterrichtsstunden Mathematik