Kapitel 1 : Teilbarkeit

1.1 Teiler und Vielfache

Lambacher Schweizer: "Mathematik für Gymnasien Klasse 6" [ISBN: 978-3-12-733267-4]
Klett Verlag : Lambacher Schweizer Mathematik 6
Wikipedia : Zahlengerade

1.0 Teiler und Vielfache

Zahlen ordnen und vergleichen

Zahlengerade
Alle Zahlen lassen sich auf einer Zahlengeraden abbilden:
Definition:
"Eine Zahlengerade ist eine Gerade, auf der Striche in gleichen Abständen voneinander
abgetragen werden. Jeder Strich steht für eine Zahl. Die Zahlengerade kann positive und
negative Zahlen enthalten."

Darstellung einer Zahlengeraden:

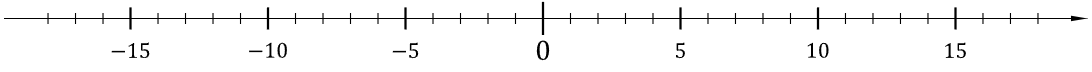
Auf dieser Zahlengeraden stehen die senkrechten Striche für ganze Zahlen: $Zahl \in \mathbb{Z}$
Die Menge $M$ der Zahlen $M = \{..,-15,-10,-5,0,+5,+10,+15,..\}$ sind ganzzahlige Vielfache der Zahl $5$ :
$M = \{..,-15,-10,-5,0,+5,+10,+15,..\} = \{..,-3 \cdot 5,-2 \cdot 5,-1 \cdot 5,0 \cdot 5,+1 \cdot 5,+2 \cdot 5,+3 \cdot 5,..\}$

Wichtig:
"Die Zwischenräume zwischen den senkrechten Strichen stellen eine
unendliche Menge von Kommazahlen dar."

So liegt zwischen den Strichen $2$ und $3$ die Zahl $2.451298234$ :

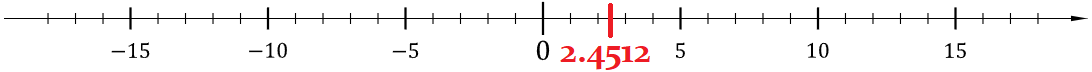
Wichtig:
"Die Zahlen auf der Zahlengeraden besitzen eine eindeutige Zuordnung:
eine Zahl links von einer anderen Zahl rechts ist immer kleiner!"
Daher sind die Zahlen auf der Zahlengeraden von ihrer Grösse von links (klein)
nach rechts (gross) sortiert aufgetragen!

Schwieriger Fall: wie trage ich Brüche auf der Zahlengeraden ein?
Bruch-Beispiel: $\dfrac{3}{2} = 3 : 2 = 1.5$
Bruch-Beispiel: $\dfrac{5}{7} = 5 : 7 = 0.\overline{714285}$
Daher rechnen wir den Bruch durch schriftliche Division oder mit Taschenrechner aus:
Die Division von Zähler(ganze Zahl) durch Nenner(ganze Zahl) ergibt eine rationale Zahl:
$\dfrac{a}{b} = a : b = c$ mit $\{a,b\} \in \mathbb{Z}$ und $c \in \mathbb{Q}$
Die durch die Division erhaltene Kommazahl kann dann auf dem Zahlenstrahl dargestellt werden!
Mit dieser Vorschrift der Division Zähler durch Nenner lassen sich Brüche dann auch der Grösse nach sortieren!

Multiplikationstabelle

Aufgabe: Konstruiere eine Multiplikationstabelle der natürlichen Zahlen bis $10$:

Lösung:
  • Schreibe die Zahlen von 1 bis 10 als Tabellenzeile
  • Schreibe die Zahlen von 1 bis 10 als Tabellenspalte
  • Schreibe das Produkt von Zahl-Zeile mal Zahl-Spalte in die entsprechende Tabellenzelle

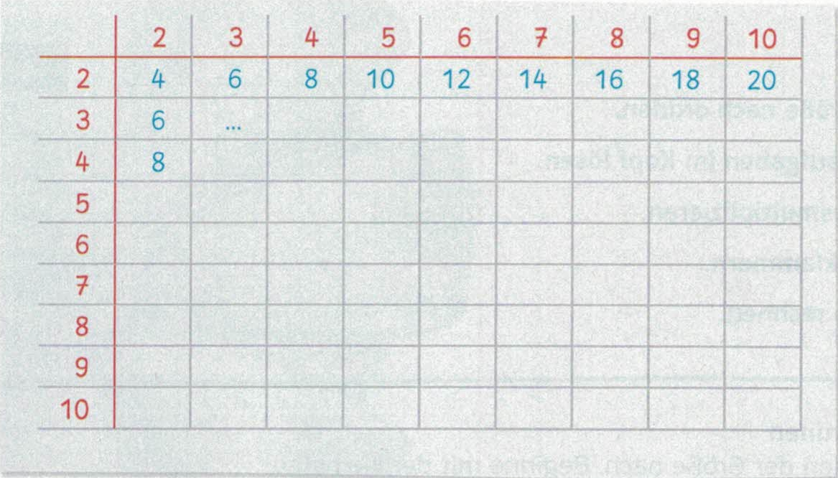
Bemerkung: Aus Platzgründen wird die Zahl $1$ nicht mit in der Tabelle aufgeführt!

Multiplikationsbaum

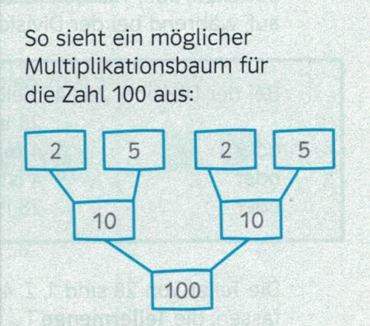
Aufgabe: Konstruiere einen Multiplikationsbaum für die Faktoren der Zahl $100$:

Lösung:
  • Schreibe die Zahl $100$ in die Mitte der untersten Zeile.
  • Faktorisiere $100 = 10 \cdot 10$ und schreibe beide Faktoren in die nächst höhere Zeile.
  • Faktorisiere $10 = 2 \cdot 5$ und schreibe die Faktoren in die nächst höhere Zeile.
  • [Stoppe, wenn keine echten Teiler mehr gefunden werden.]

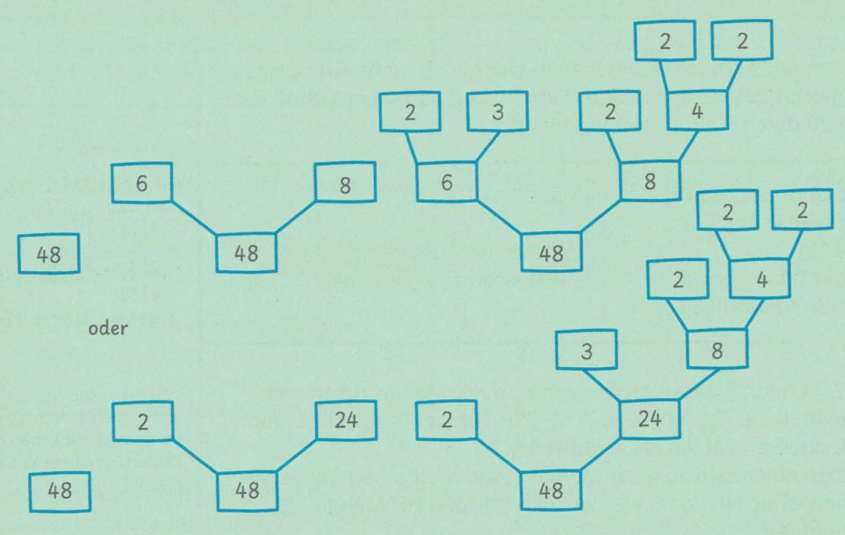
Aufgabe: Konstruiere verschiedene Multiplikationsbäume für die Faktoren der Zahl $48$:

Zahlen auf ihren Teiler untersuchen

Echte Teiler und unechte Teiler

Teilermenge / Vielfachenmenge

Definition:
"Ein Teiler ist eine Zahl $z \in \mathbb{Z}$, durch die man eine andere Zahl $x \in \mathbb{Z}$ ganzzahlig ohne Rest teilen kann."

Definition:
"Eine Teilermenge(Vielfachenmenge) ist die Menge der Zahlen, durch die man eine Zahl $z \in \mathbb{Z}$ ganzzahlig
teilen kann, also ohne dass ein Rest bleibt."

Definition:
"Echte Teiler sind alle Teiler einer Zahl, die ungleich der Zahl selbst und $1$ sind."
"Jede ganze Zahl $z \in \mathbb{Z}$ hat mindestens zwei Teiler, nämlich $1$ und sich selbst."
"Alle anderen Teiler werden als echte Teiler bezeichnet."

Beispiel: Teilbarkeit
Ist $117$ durch $7$ teilbar?
$117 : 7 = 16 R 5$ denn $16 \cdot 7 + 5 = 112 + 5 = 117$

Beispiel: Teilbarkeit
Ist $35$ durch $7$ teilbar?
$35 : 7 = 5 R 0$ denn $5 \cdot 7 + 0 = 35 + 0 = 35$

Beispiel: Teiler/Teilermenge
$15 = 1 \cdot 15 = 3 \cdot 5$
$\Rightarrow 1,15$ sind unechte Teiler von $15$
$\Rightarrow 3,5$ sind echte Teiler von $15$
$\Rightarrow \{3,5\}$ ist die Teilermenge von $15$

Beispiel: Teiler/Teilermenge
$4 = 1 \cdot 4 = 2 \cdot 2$
$\Rightarrow 1,4$ sind unechte Teiler von $4$
$\Rightarrow 2$ ist echter Teiler von $4$
$\Rightarrow \{2\}$ ist die Teilermenge von $125$

Beispiel: Teiler/Teilermenge
$8 = 2 \cdot 2 \cdot 2$
$\Rightarrow 2$ ist echter Teiler von $8$
$\Rightarrow \{2\}$ ist die Teilermenge von $125$

Beispiel: Teiler/Teilermenge
$125 = 5 \cdot 5 \cdot 5$
$\Rightarrow 5$ ist echter Teiler von $125$
$\Rightarrow \{5\}$ ist die Teilermenge von $125$

Beispiel: Teiler/Teilermenge
$210 = 2 \cdot 3 \cdot 5 \cdot 7$
$\Rightarrow 2,3,5,7$ sind echte Teiler von $210$
$\Rightarrow \{2,3,5,7\}$ ist die Teilermenge von $210$

Bemerkung: Teiler/Teilermenge
Die Zerlegung einer ganzen Zahl $z \in \mathbb{Z}$ in ein Produkt kleinstmöglicher echter Teiler heisst Primfaktorzerlegung.
Die Menge der kleinstmöglichen Faktoren sind Primzahlen.

Teilbarkeit durch Zerlegung in Summe oder Differenz

Teilbarkeit durch Summenzerlegung
Beispiel: Teilbarkeit durch Summenzerlegung von $714$
Frage: Ist $714$ durch $21$ teilbar?
Trick: $30 \cdot 21 = 630$ : Wahl einer Teilsumme $630$ mit Teiler $21$
Bilde Summe: $714 = 630 + 84$
Prüfe zweiten Summanden $84$ auf Teilbarkeit mit $21$ $\Rightarrow 84 = 4 \cdot 21$ (q.e.d)
Ergebnis: $714 = 630 + 84 = 30 \cdot 21 + 4 \cdot 21 = (30 + 4) \cdot 21 = 34 \cdot 21$
Damit ist $714$ insgesamt $34$ mal durch $21$ teilbar!

Teilbarkeit durch Differenzerlegung
Beispiel: Teilbarkeit durch Differenzzerlegung von $714$
Frage: Ist $714$ durch $21$ teilbar?
Trick: $40 \cdot 21 = 840$ : Wahl einer Teilsumme $840$ mit Teiler $21$
Bilde Differenz: $714 = 840 - (40 + 86) = 840 - 126$
Prüfe Subtrahend $126$ auf Teilbarkeit mit $21$ $\Rightarrow 126 = 6 \cdot 21$ (q.e.d)
Ergebnis: $714 = 840 - 126 = 40 \cdot 21 - 6 \cdot 21 = (40 - 6) \cdot 21 = 34 \cdot 21$
Damit ist $714$ insgesamt $34$ mal durch $21$ teilbar!

Teilbarkeit mit Taschenrechner/Computer

Beispiel 1

Frage: Ist die Zahl $z=714$ durch den Divisor $d=21$ ganzzahlig teilbar?

Lösung:
Eingabe in Taschenrechner: $714 : 21$
Ergebnis Taschenrechner: $34$ ohne Kommastellen!

Antwort: Die Zahl $z=714$ ist durch den Divisor $d=21$ ganzzahlig $34§ mal teilbar!

Beispiel 2

Frage: Ist die Zahl $z=123$ durch den Divisor $d=21$ ganzzahlig teilbar?

Lösung:
Eingabe in Taschenrechner: $123 : 21$
Ergebnis Taschenrechner: $5.\overline{857142}$ mit Kommastellen!

Antwort: Die Zahl $z=123$ ist durch den Divisor $d=21$ nicht ganzzahlig teilbar!

Zahlen als Produkt von Faktoren darstellen

Folgerung:
"Jede ganze Zahl $z \in \mathbb{Z}$ kann als Produkt von $1$ und der Zahl selbst dargestellt werden: $z = 1 \cdot z$ "
"$1$ und $z$ sind unechte Teiler von $z$"

Folgerung:
"Jede ganze Zahl $z \in \mathbb{Z}$ kann als Produkt von $1$ und der Zahl selbst dargestellt werden: $z = 1 \cdot z$ "

Beispiel: Teilbarkeit von Schokolade

Aufteilung in gleiche Portionen:
Tafel (1) : $3 \cdot 4$ , $2 \cdot 6$ Stücke $[12 = 3 \cdot 4 = 3 \cdot 2 \cdot 2]$
Tafel (2) : $5 \cdot 5$ Stücke $[25 = 5 \cdot 5]$
Tafel (3) : $4 \cdot 5$ Stücke $[20 = 4 \cdot 5]$
Tafel (4) : $2 \cdot 6$ , $3 \cdot 4$ Stücke $[12 = 3 \cdot 4 = 3 \cdot 2 \cdot 2]$
Tafel (5) : $4 \cdot 4$ , $2 \cdot 8$ Stücke $[16 = 4 \cdot 4 = 2 \cdot 2 \cdot 2 \cdot 2]$

Homepage WebSites Unterrichtsstunden Mathematik