Kapitel 1 : Merkmale der Physik
1.1 Was ist Physik?
1.2 Physik und Mathematik
1.3 Vorgehensweise: Grundgleichungen der Mechanik
1.4 Vorgehensweise: Erhaltungsgrössen
Quellen
Wikipedia : Konstante
Wikipedia : Einheit
Wikipedia : Variable
Wikipedia : Term (Algebra)
Wikipedia : Gleichung
Wikipedia : Klammer (Zeichen)
1.2 Physik und Mathematik
Mathematische Grundstrukturen mit Beispielen:
• Konstante (Constant)
• Einheit (Unit)
• Variable (Variable)
• Term (Term)
• Gleichung (Equation)
• Klammern (Brackets)
Definition: Konstante (Constant)
• Konstante werden für ein bestimmtes Problem definiert
und sind innerhalb dieses Problemvolumens unveränderbar.
Eine Konstante wird geschrieben:
• als Zahl ohne Einheit oder
• als Zahl mit Einheit oder
• als Buchstabe: dieser Buchstabe steht für die symbolhafte Abkürzung
der definierten konstanten Zahl mit oder ohne Einheit(typisch als $C$) !
• Alle Zahlenbereiche sind für Konstante zulässig:
$C \in \mathbb{N}$ oder $C \in \mathbb{Z}$ oder $C \in \mathbb{Q}$ oder $C \in \mathbb{I}$ oder $C \in \mathbb{R}$
Beispiele: Konstante Zahl
• Natürliche Zahl: $5 \in \mathbb{N}$ $\Rightarrow ~~C = 5$
• Ganze Zahl: $-3 \in \mathbb{Z}$ $\Rightarrow ~~C = -3$
• Rationale Zahl: $1.234 \in \mathbb{Q}$ $\Rightarrow ~~C = 1.234$
• Rationale Zahl: $-7.\overline{23} = -7.2323.. \in \mathbb{Q}$ $\Rightarrow ~~C = -7.\overline{23}$
• Rationale Zahl: $\dfrac{3}{7} \in \mathbb{Q}$ $\Rightarrow ~~C = \dfrac{3}{7}$
• Irrationale Zahl: $\pi \in \mathbb{I}$ $\pi = 3.14159265359.. \Rightarrow ~~C = \pi$
• Irrationale Zahl: $\sqrt{2} \in \mathbb{Q}$ $\sqrt{2} = 1.41421356237.. \Rightarrow ~~C = \sqrt{2}$
Beispiele: Konstante Zahl mit Einheit
• Erdbeschleunigung $g \in \mathbb{R}$ $g = 9.81 \dfrac{m}{s^2}$
Wikipedia: Erdbeschleunigung
• Naturkonstante: Gravitationskonstante $G \in \mathbb{R}$ $G = 6.67430 \cdot 10^{-11} \dfrac{m^3}{kg \cdot s^2}$
Wikipedia: Gravitationskonstante
Definition: Einheit (Unit)
Regeln:
WICHTIG! Eine Einheit wird als Faktor bei der Zahl (Messgrösse) geschrieben !!!
Messung einer Strecke: $\boxed{S = 3.01 m ~\Leftrightarrow~ S = 3.01 \cdot m}$ ("$m$" steht für Meter)
Messung einer Zeit: $\boxed{T = 1.98 s ~\Leftrightarrow~ S = 1.98 \cdot s}$ ("$s$" steht für Sekunden)
WICHTIG: Zur Minimierung der Schreibarbeit wird der Multiplikationspunkt "$\cdot$" weggelassen !!!
WICHTIG! Zahl mal Einheit unterliegt als Produkt den bisher bekannten Produkt-Rechenregeln !!!
WICHTIG! SONDERFALL! Behauptung: Auch Zahlen OHNE Einheit besitzen die Einheit "1" !!!
Bei der Zahl $3.2$ steht zwar keine Einheit, doch wir erweitern:
$3.2 = 3.2 \cdot 1$
Wegen der "$1$" als neutralem Element der Multiplikation besitzt jede Zahl ohne Einheit die Einheit "$1$" !!!
Beispiel einer Messung zur Berechnung der Geschwindigkeit:
Eine (gemessene) Strecke $s$ beträgt: $\boxed{s = 3.01 m}$ ("$m$" steht für Meter)
Eine (gemessene) Zeit $t$ beträgt: $\boxed{t = 1.98 s}$ ("$s$" steht für Sekunde(n))
Die daraus sich ergebene Geschwindigkeit $v$ beträgt:
Geschwindigkeit $v$ gleich Weg $s$ durch Zeit $t$
$\boxed{v := \dfrac{s}{t}}$ $\Leftrightarrow$ $v = \dfrac{3.01 m}{1.98 s}$ $\Leftrightarrow$ $v = \dfrac{3.01 \cdot m}{1.98 \cdot s}$ $\Leftrightarrow$ $v = \dfrac{3.01}{1.98} \cdot \dfrac{m}{s}$ $\Leftrightarrow$ $\boxed{v = 1.52 \dfrac{m}{s}}$
("$v$" : Latein: velocitas/velocitatis : Geschwindigkeit)
("$\dfrac{m}{s}$" steht für Meter pro Sekunde)
Möglichkeit zur "Berechnung" der Einheit einer Variablen:
Der Operator $[~]$ angewendet auf eine Variable oder eines mathemathischen Ausdrucks
liefert nur die physikalische Einheit desselben ohne Zahl.
Beispiel: $v = 1.52 \dfrac{m}{s} ~~\rightarrow ~~ [v] = \dfrac{m}{s}$
Beispiel: $v := \dfrac{s}{t} ~~\rightarrow ~~ [v] = [\dfrac{s}{t}] = \dfrac{[s]}{[t]} = \dfrac{m}{s}$ da $[s] = m$ und $[t] = s$
Umrechnung von Einheiten:
Umrechnung von Sekunden in Minuten und umgekehrt:
$\boxed{1m = 60s} \Leftrightarrow 1 \cdot m = 60 \cdot s~~\big\vert~~$ Malpunkt zwischen Wert und Einheit! auf beiden Seiten: $: 60$
$\dfrac{1}{60} \cdot m = \dfrac{60}{60} \cdot s = 1 \cdot s = 1s ~~\Rightarrow \boxed{\dfrac{1}{60} m = 1s}$
Umrechnung von Metern in Kilometern und umgekehrt:
$\boxed{1km = 1000m} \Leftrightarrow 1 \cdot km = 1000 \cdot m ~~\big\vert~~$ Malpunkt zwischen Wert und Einheit! auf beiden Seiten: $: 1000$
$\dfrac{1}{1000} \cdot km = \dfrac{1000}{1000} \cdot m = 0.001 \cdot km = 1m ~~\Rightarrow \boxed{\dfrac{1}{1000} km = 0.001 km = 1m}$
Umrechnung von Kilometern pro Stunde in Meter pro Sekunde:
$1\dfrac{km}{h} = ? \dfrac{m}{s}$
$1\dfrac{km}{h} = \dfrac{1000 \cdot m}{3600 \cdot s} = \dfrac{1000}{3600} \cdot \dfrac{m}{s}$
$\boxed{1\dfrac{km}{h} = \dfrac{1000}{3600} \dfrac{m}{s} = 0.2\overline{7} \dfrac{m}{s}}$
Umrechnung von Metern pro Sekunde in Kilometer pro Stunde:
$1 \dfrac{m}{s}= ? \dfrac{km}{h}$
$1 \dfrac{km}{h}= \dfrac{1000 \cdot m}{3600 \cdot s} ~~\big\vert \cdot \dfrac{3600}{1000}$
$1 \cdot \dfrac{km}{h} \cdot \dfrac{3600}{1000}= \dfrac{1000 \cdot m}{3600 \cdot s} \cdot \dfrac{3600}{1000}$
$1 \cdot \dfrac{3600}{1000} \cdot \dfrac{km}{h}= \dfrac{1000 \cdot 3600}{ 3600 \cdot 1000} \cdot \dfrac{m}{s} = 1 \cdot \dfrac{m}{s}$
$\dfrac{3600}{1000} \cdot \dfrac{km}{h} = 1 \cdot \dfrac{m}{s}$
$\boxed{1 \dfrac{m}{s} = \dfrac{3600}{1000} \dfrac{km}{h} = 3.6 \dfrac{km}{h}}$
Definition: Variable (Variable)
Wikipedia: Variable (Mathematik) :
"Eine Variable ist ein Name für eine Leerstelle in einem logischen oder mathematischen Ausdruck."
Wikipedia: Variable (Programmierung) :
"In der Programmierung ist eine Variable ein abstrakter Behälter für einen Wert, der bei der Ausführung eines Computerprogramm auftritt."
Unsere Definition für eine Variable in der Mathematik, Physik und Informatik:
"Eine Variable ist ein Name für den Platzhalter einer Zahl in einem logischen oder mathematischen Ausdruck."
Jede Variable besitzt einen (eindeutigen) Namen.
Jede Variable besitzt eine (interne) Einheit:
• keine oder neutrale Einheit "$1$" (wird als Faktor weggelassen!)
• eine physikalische Einheit wie
• Sekunde "$s$" (Zeit)
• Meter "$m$" (Länge)
• Kilogramm "$kg$" (Masse)
• Ampere "$A$" (Stromstärke)
• Kelvin "$K$" (Temperatur)
• Mol "$mol$" (Stoffmenge, Chemie)
• Candela "$cd$" (Lichtstärke)
Die Berechnung der Einheit einer Variable erfolgt durch den Operator $[~]$:
Beispiel: $s = 3.01 m ~~\rightarrow ~~ [s] = m$
(Der Operator $[~]$ liefert nur die physikalische Einheit einer Variablen ohne seine Zahl.)
Beispiele: Variablen in Gleichungen
• $\boxed{x + 3 = 5}$
Typische Bestimmungsgleichung für die Variable $x$ .
• $\boxed{y = 5 - 12}$
Typische Bestimmungsgleichung für die Variable $y$ .
• $\boxed{x + y = 12}$
Die beiden Variablen $x$ und $y$ sollen addiert $12$ ergeben.
• $\boxed{a \cdot x + b \cdot y = c}$
Mit den bekannten Konstanten $a,b,c \in \mathbb{R}$ beschreiben die beiden Variablen $x$ und $y$ eine Gerade.
• $\boxed{x^2 + y^2 = c^2}$
Die Summe der Quadrate $x^2$ und $y^2$ ergeben die bekannte Konstante $c \in \mathbb{R}$
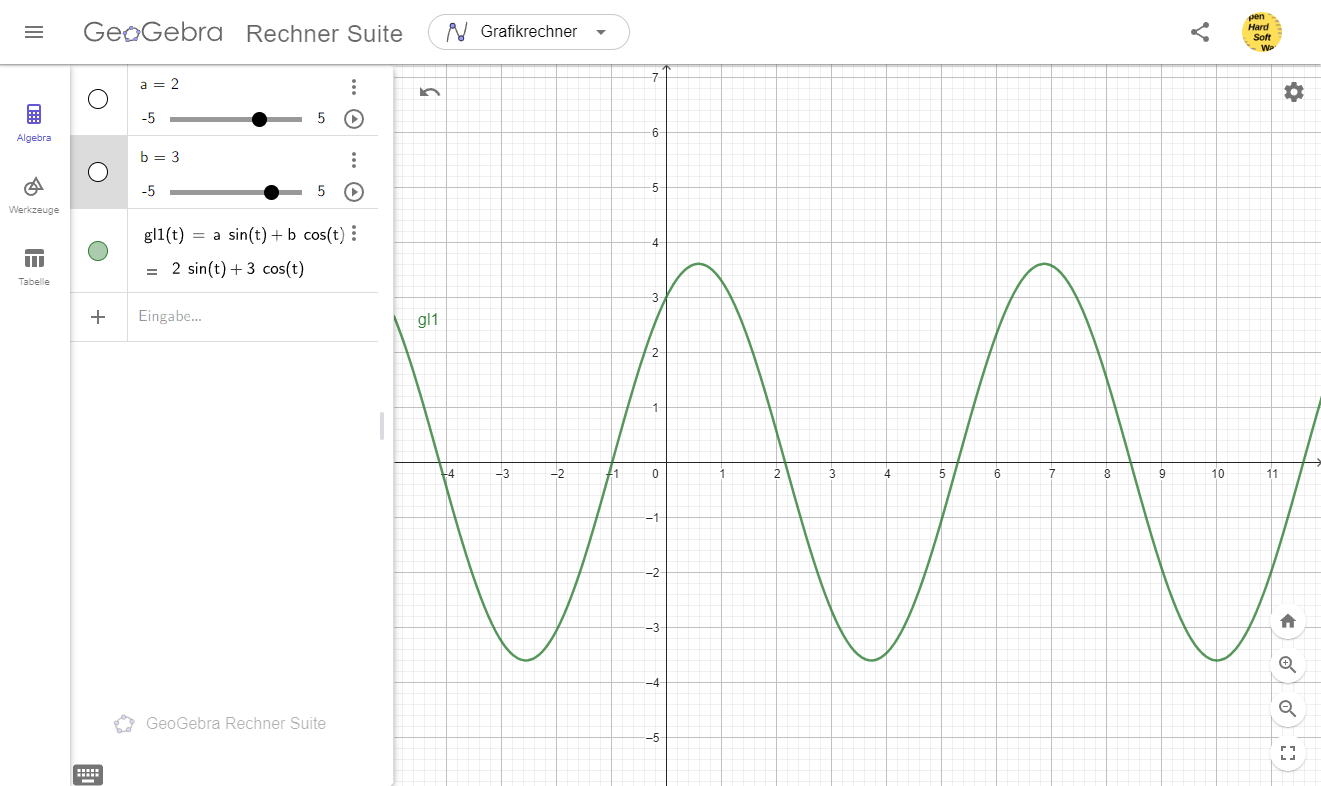
• $\boxed{x(t) = a \cdot \sin(t) + b \cdot \cos(t)}$
Die Weg-Zeit-Funktion $x(t)$ : $x$-Weg in Abhängigkeit der Zeit $t$ setzt sich zusammen aus dem
Produkt $a \cdot \sin(t)$ einer Sinus-Zeit-Funktion und dem Produkt $b \cdot \cos(t)$ einer Cosinus-Zeit-Funktion.
$a, b \in \mathbb{R}$ sind Konstante (bezüglich der Zeit).
Diese Gleichung lässt sich auch mit GeoGebra grafisch darstellen:
Definition: Term (Term)
"Unter einem algebraischen Term verstehen wir eine endliche Reihung von Konstanten "$C, G, g, ...$" und Variablen "$x, y, z, w^2, ...$" und Operatoren "$+,-,\cdot,/,...$" oder "$(,),[,],...$" ohne Gleichheitszeichen"
Terme mit einer Variablen
Beispiele: $2x+7$, $\dfrac{3}{y}$, $z^3 + 3z + 2$
Terme mit mehreren Variablen
Beispiele: $2x+7y+21$, $\dfrac{3x}{y^2}$, $x^3 + 3y + 2z$
Rechenregel: Zusammenfassung gleicher Variablen
Term: $2x + 4x$
Berechnung von Termen
Wenn alle Konstanten und Variablen in einem Term durch Zahlen definiert und damit bekannt sind, kann dieser Term berechnet werden.
Beispiel: $2x + 3y^2$ mit $x=2.5$ und $y=2.0$ $~~\Rightarrow~~ 2 \cdot 2.5 + 3 \cdot 4 = 17$
Vereinfachung von Termen
Nur Terme gleicher Variablen mit gleichen Exponenten und beliebigen Vorfaktoren können zusammengefasst werden:
gemeinsamer Exponent $1$ : $2x + 3x = x \cdot x + x \cdot x \cdot x = x \cdot x \cdot x \cdot x \cdot x = 5x$
gemeinsamer Exponent $2$ : $2y^2 + 3y^2 = y^2 \cdot y^2 + y^2 \cdot y^2 \cdot y^2 = y^2 \cdot y^2 \cdot y^2 \cdot y^2 \cdot y^2 = 5 y^2$
aber: kein gemeinsamer Exponent $2 \neq 3$ : $x^2 + x^3 = x^2 + x^3$
aber: ungleiche Variablennamen $x \neq y$: $3x + 2y = 3x + 2y$
Beispiel: Vereinfache Term: $8x + 5xy + 7y -2xy +0.4y$
$8x + 5xy + 7y - 2xy + 0.4y = 8x + 5xy - 2xy + 7y + 0.4y = 8x + 3xy + 7.4y$
Beispiel: Fasse den Term $5x \cdot 2y \cdot x^2 \cdot 4 - (5y \cdot 4 - 2x^3y)$ so weit wie möglich zusammen:
$5x \cdot 2y \cdot x^2 \cdot 4 - (5y \cdot 4 - 2x^3y) = $
$= 4 \cdot 5 \cdot 2 \cdot x \cdot x^2 \cdot y - (4 \cdot 5y - 2x^3y) =$
$= 40 x^3 y + 2x^3y - 20 y = 42 x^3 y - 20 y$
Beispiel: Volumenberechnung eines Quaders:
Kantenlängen: $a = x$ und $b = 4x$ und $c = 5x$
Volumen: $\boxed{V = a \cdot b \cdot c}$
Einsetzen: $V = x \cdot 4x \cdot 5x \Rightarrow \boxed{V = 20 x^3}$
Definition: Gleichung (Equation)
"Unter einer Gleichung verstehen wir die Reihung eines Terms, eines Gleichheitszeichens
und eines weiteren Terms. Auf beiden Seiten des Gleichheitszeichens stehen gleiche Werte.
$\Rightarrow$ Damit ist der Wert von Term-Links gleich dem Wert von Term-Rechts!"
In Syntax-Notation schreiben wir: "$gleichung := ~~ = $"
Beispiel-Gleichung: $y = 3x + 2$
• "$y = 3x + 2$" entspricht: Gleichung mit Term "$y$", Gleichheitszeichen "$=$" und Term "$3x + 2$"
• Wir wählen (willkürlich) $x=2 ~~\Rightarrow~~ y=8$
Damit erhalten wir die Werte-Gleichung: $8 = 3 \cdot 2 + 2 ~~\Leftrightarrow~~8 = 8$
$\Rightarrow$ rechte Seite gleich linke Seite !
Äquivalenzumformung von Gleichungen
Oft sind Gleichungen:
• in unübersichtlicher Form gegeben -
durch Äquivalenzumformungen kann eine übersichtliche Darstellung erreicht werden.
• nicht nach der unbekannten Variablen aufgelöst -
durch Äquivalenzumformungen kann eine Auflösung nach der unbekannten Variablen erfolgen.
Beispiel-Gleichung: $\boxed{y - 3x = 2}$ (Auflösung nach $y$)
• Bringe die Gleichung in die Form einer Geradengleichung mit $y = mx + b$
$y - 3x = 2 ~~\big\vert~ +3x ~~$ [auf beiden Seiten $3x$ addieren]
$y - 3x + 3x = 2 + 3x ~~\big\vert~~$ [vereinfachen, ordnen]
$\boxed{y = 3x + 2} ~~$ : entspricht der Geradengleichung $y = mx + b$
Beispiel-Gleichung: $\boxed{2y + 3x - 12 = 2x - y}$ (Auflösung nach $y$)
• Bringe die Gleichung in die Form einer Geradengleichung mit $y = mx + b$
$5y + 3x - 12 - 3y = 2x - y ~~\big\vert~~$ [vereinfachen, ordnen]
$5y - 3y + 3x - 12 = 2x - y ~~\big\vert~~$ [vereinfachen, ordnen]
$2y + 3x - 12 = 2x - y ~~\big\vert -3x$ [auf beiden Seiten 3x abziehen]
$2y + 3x - 3x - 12 = 2x - 3x - y ~~\big\vert~~ $ [vereinfachen, ordnen]
$2y - 12 = -x - y ~~\big\vert~~ +y$ [auf beiden Seiten $y$ addieren]
$2y + y - 12 = - x - y + y ~~\big\vert~~ +y$ [vereinfachen, ordnen]
$3y - 12 = - x ~~\big\vert~~ +12$ [auf beiden Seiten $12$ addieren]
$3y - 12 + 12 = - x + 12~~\big\vert~~ +12$ [vereinfachen]
$3y = - x + 12 ~~\big\vert~~ \cdot \dfrac{1}{3}$ [auf beiden Seiten durch $3$ teilen]
$3 \cdot \dfrac{1}{3} \cdot y = - \dfrac{1}{3}x + 12 \cdot \dfrac{1}{3} ~~\big\vert$ [vereinfachen]
$\boxed{y = - \dfrac{1}{3}x + 4}$ : entspricht der Geradengleichung $y = mx + b$
Definition: Klammern (Brackets)
"Klammern sind Operatoren zur Einhaltung des Vorrangs auszuführender Rechenoperationen."
Ausmultiplizieren
Beispiel: $5 \cdot (2 + 3) = 5 \cdot 5 = 25$
Beispiel: $(7 - 2) \cdot (2 + 3) = 5 \cdot 5 = 25$
Wir merken uns: Immer erst versuchen, die Klammern in einer Gleichung zu vereinfachen!
Ausklammern
Ein Ausklammern wird zur Vereinfachung von Termen eingesetzt.
Beispiel: $ax + bx = x(a + b)$
Beispiel: $y^2 + cy = y(y + c)$
Distributivgesetz
Aber: Wie vereinfache ich folgenden Term: ?
Beispiel: $a \cdot (b + c)$
$\boxed{a \cdot (b + c) = a \cdot b + a \cdot c}$ heisst Distributivgesetz der Addition
"Produkt von $a$ mal Summe von $b$ und $c$ ist gleich der Summe von Produkt $a \cdot b$ plus Produkt $a \cdot c$" .
$\boxed{a \cdot (b - c) = a \cdot b - a \cdot c}$ heisst Distributivgesetz der Subtraktion
"Produkt von $a$ mal Differenz von $b$ minus $c$ ist gleich der Differenz von Produkt $a \cdot b$ minus Produkt $a \cdot c$" .
Veranschaulichung:
$5 \cdot (2 + 3) = 5 \cdot 5 = 25$ [direktes Ausrechnen]
$5 \cdot (2 + 3) = 5 \cdot 2 + 5 \cdot 3 = 10 + 15 = 25$ [Distributivgesetz]
Beide Rechenwege führen zum selben Ergebnis !
$5 \cdot (7 - 2) = 5 \cdot 5 = 25$ [direktes Ausrechnen]
$5 \cdot (7 - 2) = 5 \cdot 7 + 5 \cdot 2 = 35 - 10 = 25$ [Distributivgesetz]
Beide Rechenwege führen zum selben Ergebnis !
Bemerkung:
• Klammern haben eine höhere Priorität als die Regel "Punktrechnung geht vor Strichrechnung" !
• Das Distributivgesetz schreibt mit den beiden Klammern "$($" und "$)$"
die Reihenfolge der Bearbeitung der beiden Operatoren "$+/-$" und "$\cdot$" vor !
Mehrere Klammern:
Beispiel: $2 \cdot (5 \cdot (2 + 3) + 7) = 2 \cdot (5 \cdot 5 + 7) = 2 \cdot (25 + 7)= 2 \cdot 32 = 64$
Wichtig:
• Es muss immer die Zahl der Auf-Klammern gleich der Zahl der Zu-Klammern sein !
• Die Klammern werden von innen nach aussen aufgelöst !
• Es gilt auch bei der sukzessiven Klammerauflösung die Regel: "Punktrechnung geht vor Strichrechnung" !
Assoziativgesetz
$\boxed{a \cdot (b \cdot c) = (a \cdot b) \cdot c = a \cdot b \cdot c}$ heisst Assoziativgesetz
Oder anders ausgedrückt: die Reihenfolge der Berechnung der Faktoren ist beliebig !
Homepage
WebSites
Unterrichtsstunden
Physik
Beispiel-Gleichung: $y = 3x + 2$
• "$y = 3x + 2$" entspricht: Gleichung mit Term "$y$", Gleichheitszeichen "$=$" und Term "$3x + 2$"
• Wir wählen (willkürlich) $x=2 ~~\Rightarrow~~ y=8$
Damit erhalten wir die Werte-Gleichung: $8 = 3 \cdot 2 + 2 ~~\Leftrightarrow~~8 = 8$
$\Rightarrow$ rechte Seite gleich linke Seite !
Äquivalenzumformung von Gleichungen
Oft sind Gleichungen:
• in unübersichtlicher Form gegeben -
durch Äquivalenzumformungen kann eine übersichtliche Darstellung erreicht werden.
• nicht nach der unbekannten Variablen aufgelöst -
durch Äquivalenzumformungen kann eine Auflösung nach der unbekannten Variablen erfolgen.
Beispiel-Gleichung: $\boxed{y - 3x = 2}$ (Auflösung nach $y$)
• Bringe die Gleichung in die Form einer Geradengleichung mit $y = mx + b$
$y - 3x = 2 ~~\big\vert~ +3x ~~$ [auf beiden Seiten $3x$ addieren]
$y - 3x + 3x = 2 + 3x ~~\big\vert~~$ [vereinfachen, ordnen]
$\boxed{y = 3x + 2} ~~$ : entspricht der Geradengleichung $y = mx + b$
Beispiel-Gleichung: $\boxed{2y + 3x - 12 = 2x - y}$ (Auflösung nach $y$)
• Bringe die Gleichung in die Form einer Geradengleichung mit $y = mx + b$
$5y + 3x - 12 - 3y = 2x - y ~~\big\vert~~$ [vereinfachen, ordnen]
$5y - 3y + 3x - 12 = 2x - y ~~\big\vert~~$ [vereinfachen, ordnen]
$2y + 3x - 12 = 2x - y ~~\big\vert -3x$ [auf beiden Seiten 3x abziehen]
$2y + 3x - 3x - 12 = 2x - 3x - y ~~\big\vert~~ $ [vereinfachen, ordnen]
$2y - 12 = -x - y ~~\big\vert~~ +y$ [auf beiden Seiten $y$ addieren]
$2y + y - 12 = - x - y + y ~~\big\vert~~ +y$ [vereinfachen, ordnen]
$3y - 12 = - x ~~\big\vert~~ +12$ [auf beiden Seiten $12$ addieren]
$3y - 12 + 12 = - x + 12~~\big\vert~~ +12$ [vereinfachen]
$3y = - x + 12 ~~\big\vert~~ \cdot \dfrac{1}{3}$ [auf beiden Seiten durch $3$ teilen]
$3 \cdot \dfrac{1}{3} \cdot y = - \dfrac{1}{3}x + 12 \cdot \dfrac{1}{3} ~~\big\vert$ [vereinfachen]
$\boxed{y = - \dfrac{1}{3}x + 4}$ : entspricht der Geradengleichung $y = mx + b$
Definition: Klammern (Brackets)
"Klammern sind Operatoren zur Einhaltung des Vorrangs auszuführender Rechenoperationen."
Ausmultiplizieren
Beispiel: $5 \cdot (2 + 3) = 5 \cdot 5 = 25$
Beispiel: $(7 - 2) \cdot (2 + 3) = 5 \cdot 5 = 25$
Wir merken uns: Immer erst versuchen, die Klammern in einer Gleichung zu vereinfachen!
Ausklammern
Ein Ausklammern wird zur Vereinfachung von Termen eingesetzt.
Beispiel: $ax + bx = x(a + b)$
Beispiel: $y^2 + cy = y(y + c)$
Distributivgesetz
Aber: Wie vereinfache ich folgenden Term: ?
Beispiel: $a \cdot (b + c)$
$\boxed{a \cdot (b + c) = a \cdot b + a \cdot c}$ heisst Distributivgesetz der Addition
"Produkt von $a$ mal Summe von $b$ und $c$ ist gleich der Summe von Produkt $a \cdot b$ plus Produkt $a \cdot c$" .
$\boxed{a \cdot (b - c) = a \cdot b - a \cdot c}$ heisst Distributivgesetz der Subtraktion
"Produkt von $a$ mal Differenz von $b$ minus $c$ ist gleich der Differenz von Produkt $a \cdot b$ minus Produkt $a \cdot c$" .
Veranschaulichung:
$5 \cdot (2 + 3) = 5 \cdot 5 = 25$ [direktes Ausrechnen]
$5 \cdot (2 + 3) = 5 \cdot 2 + 5 \cdot 3 = 10 + 15 = 25$ [Distributivgesetz]
Beide Rechenwege führen zum selben Ergebnis !
$5 \cdot (7 - 2) = 5 \cdot 5 = 25$ [direktes Ausrechnen]
$5 \cdot (7 - 2) = 5 \cdot 7 + 5 \cdot 2 = 35 - 10 = 25$ [Distributivgesetz]
Beide Rechenwege führen zum selben Ergebnis !
Bemerkung:
• Klammern haben eine höhere Priorität als die Regel "Punktrechnung geht vor Strichrechnung" !
• Das Distributivgesetz schreibt mit den beiden Klammern "$($" und "$)$"
die Reihenfolge der Bearbeitung der beiden Operatoren "$+/-$" und "$\cdot$" vor !
Mehrere Klammern:
Beispiel: $2 \cdot (5 \cdot (2 + 3) + 7) = 2 \cdot (5 \cdot 5 + 7) = 2 \cdot (25 + 7)= 2 \cdot 32 = 64$
Wichtig:
• Es muss immer die Zahl der Auf-Klammern gleich der Zahl der Zu-Klammern sein !
• Die Klammern werden von innen nach aussen aufgelöst !
• Es gilt auch bei der sukzessiven Klammerauflösung die Regel: "Punktrechnung geht vor Strichrechnung" !
Assoziativgesetz
$\boxed{a \cdot (b \cdot c) = (a \cdot b) \cdot c = a \cdot b \cdot c}$ heisst Assoziativgesetz
Oder anders ausgedrückt: die Reihenfolge der Berechnung der Faktoren ist beliebig !
Homepage WebSites Unterrichtsstunden Physik