1.Kapitel : Körper und Stoffe
1.1 Messung physikalischer Grössen
1.2 Beschreibung von Körpern
1.3 Masse
1.4 Dichte von Stoffen
Quellen
Schmöger, Stötzer: "Impulse Physik Klasse 7/8" [ISBN: 978-3-12-772542-1]Klett Verlag : Impulse Physik 7/8
Wikipedia : Aggregatzustand
LEIFIphysik : Volumenbestimmung
1.2 Beschreibung von Körpern
Körper und Stoff
Definition: KörperEin Körper $K$ besteht aus eine Ansammlung von Stoffen $K = \sum\limits_{i=1}^N S_i~$, nimmt ein Volumen $V$ ein und besitzt eine Masse $M$.
Beispiel Körper: Metall Eisen
Beispiel Körper: Holz Eiche
Beispiel Körper: Wasser : $K_{wasser} = \sum\limits_{i=1}^2 S_i = S_{wasserstoff} + S_{sauerstoff}$
Beispiel Körper: Milch : $K_{milch} = \sum\limits_{i=1}^3 S_i = S_{wasserstoff} + S_{sauerstoff} + S_{fett}$
Beispiel Körper: Luft : $K_{luft} = \sum\limits_{i=1}^3 S_i = S_{sauerstoff} + S_{stickstoff} + S_{kohlendioxid}$
Satz: Körper und Aggregatzustände
Definition: Arten von Aggregatzuständen
Es gibt vier Aggregatzustände:
• Fest : Festkörper nur leichte Schwingungen der Atome um die Ruhelage, geringe Geschwindigkeiten.
Beispiel: Hammer ist fest
• Flüssig : Atome sind nicht mehr im Mittel ortsfest, sondern verschiebbar.
Beispiel: Milch ist flüssig
• Gasförmig : Atome haben keine Bindung mehr und gewegen sich mit hoher Geschwindigkeit durch den Raum.
Beispiel: Luft ist gasförmig
• Plasma : sehr hohen Temperaturen spalten Atome in Atomkerne und freie Elektronen auf.
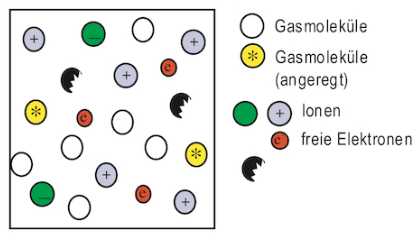
Beispiele: Plasmasäule in der Neonlampe, Plasmafaden eines Blitzes
Körper brauchen Raum
• Feste, flüssige und gasförmige Körper nehmen ein Volumen $V$ ein.• Alle Körper beanspruchen ein Volumen $V$ proportional zu ihrer Masse $M$.
• Zwei nicht identische Körper können niemals an derselben Stelle sein.
• Körper sind einmalig und damit eindeutig und beanspruchen Raum und besitzen Masse.
aber: Eindeutigkeit bezieht sich auch auf physikalische Eigenschaften von Körpern:
Verschiedene Pakete Zucker mit jeweils 1kg verhalten sich ähnlich aber nicht identisch beim beim freien Fall.
Experiment: Eintauchen des Körpers einer Kugel in einen Messzylinder
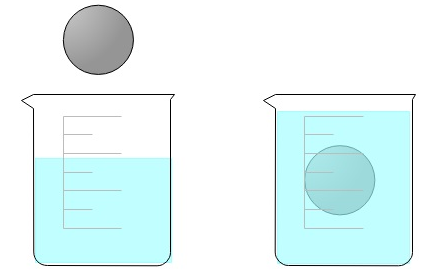
Volumen als physikalische Grösse
• Beispiel: QuaderGleichung : $\boxed{V_{quader} = l \cdot b \cdot h}$
Einheit : $~~~~~\boxed{[V_{quader}] = m \cdot m \cdot m = m3}$
• Beispiel: Würfel
Gleichung : $\boxed{V_{wuerfel} = a \cdot a \cdot a}$
Einheit : $~~~~~\boxed{[V_{wuerfel}] = m \cdot m \cdot m = m^3}$
• Beispiel: Kugel
Gleichung : $\boxed{V_{kugel} = \dfrac{4}{3} \pi r^3}$
Einheit : $~~~~~\boxed{[V_{kugel}] = [\dfrac{4}{3}] [\pi] [r^3] = 1 \cdot 1 \cdot m \cdot m \cdot m = m^3}$
Volumenbestimmung bei Flüssigkeiten
Messzylinder

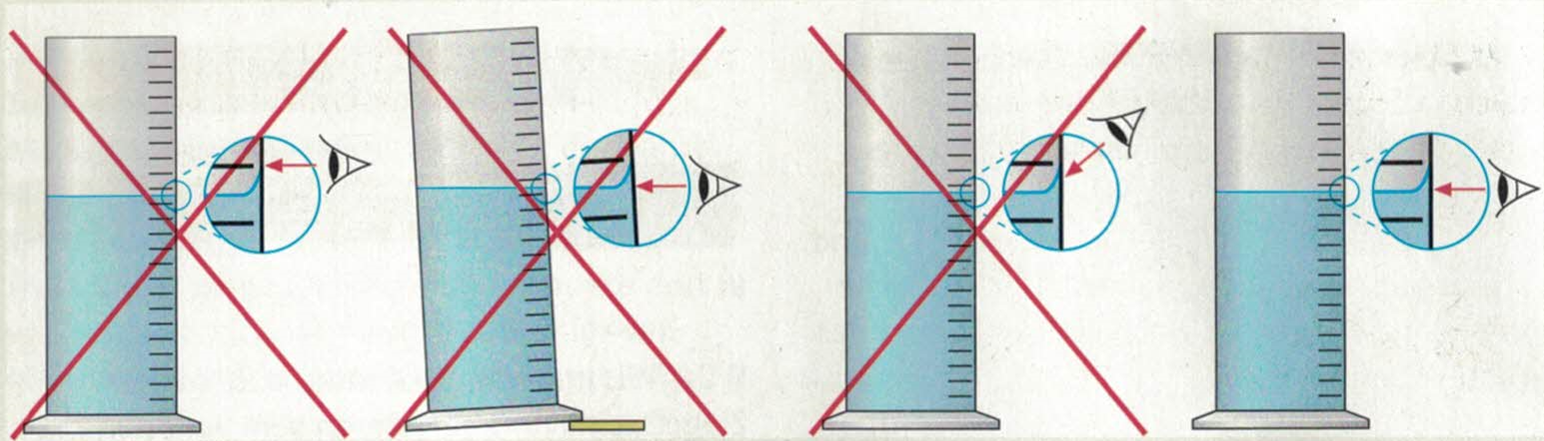
Richtiges Messen mit Messzylindern

Volumenbestimmung bei unregelmässig geformten Behältern
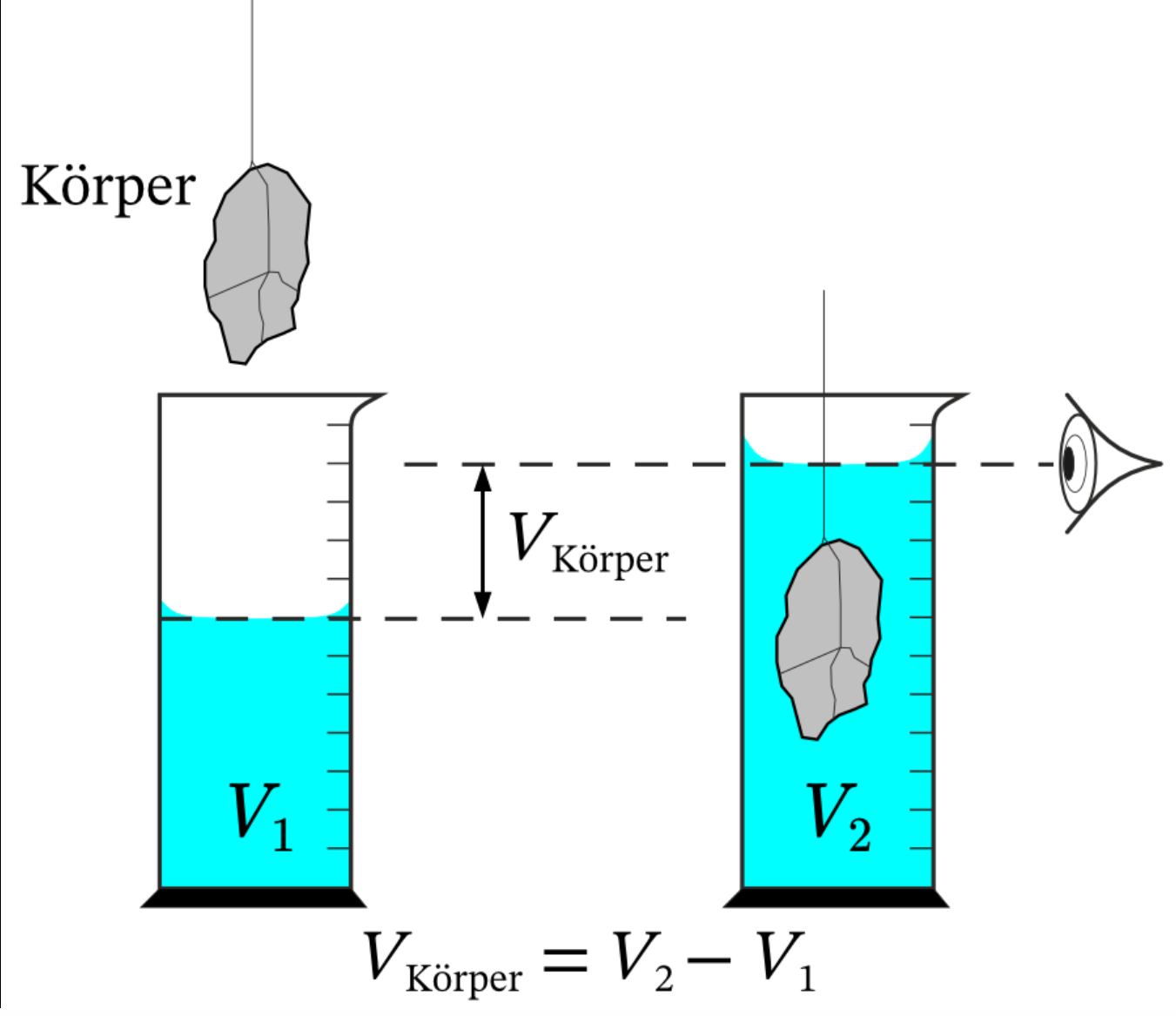
Satz: Ein nicht in der Flössigkeit löslicher Körper verdrängt genauso viel Volumen dieser Flüssigkeit wie sein eigenes Volumen, da Teile des Körpers und Teile der Flüssigkeit nicht am selben Ort sein können.Volumenbestimmung: Differenzmethode
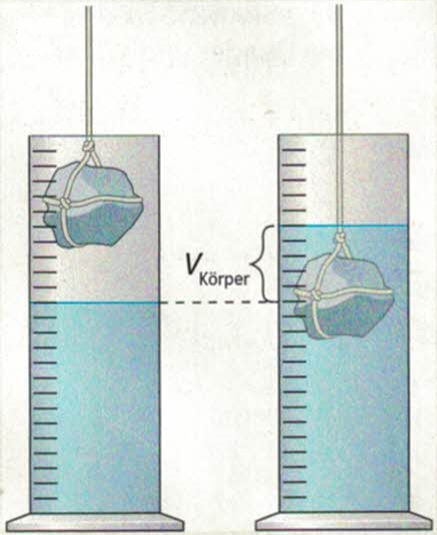
Volumenbestimmung: Überlaufmethode
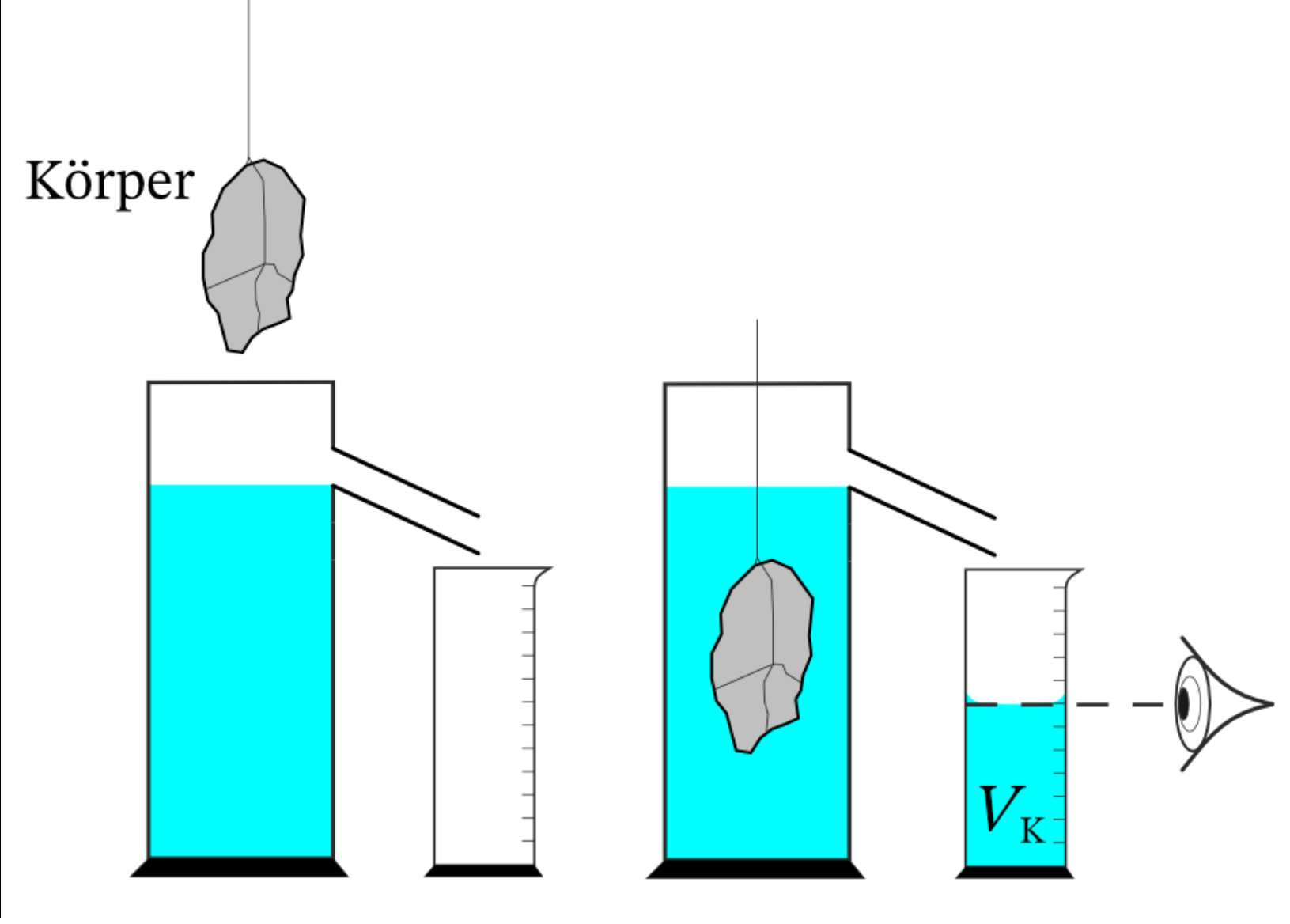
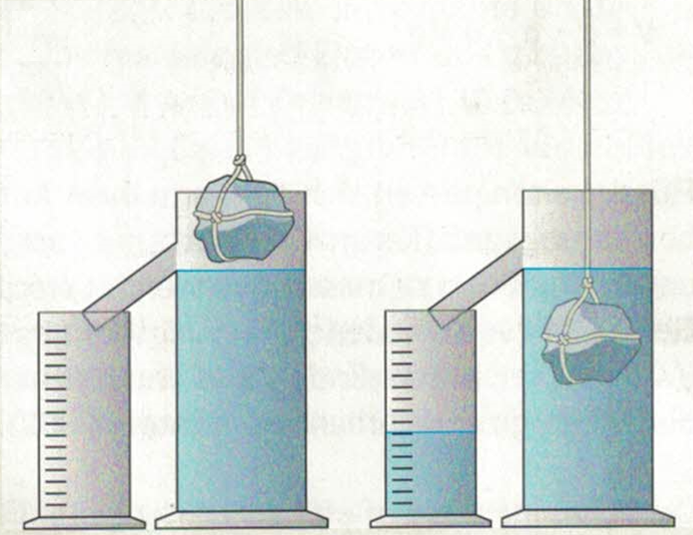
Volumenbestimmung: Atemvolumen
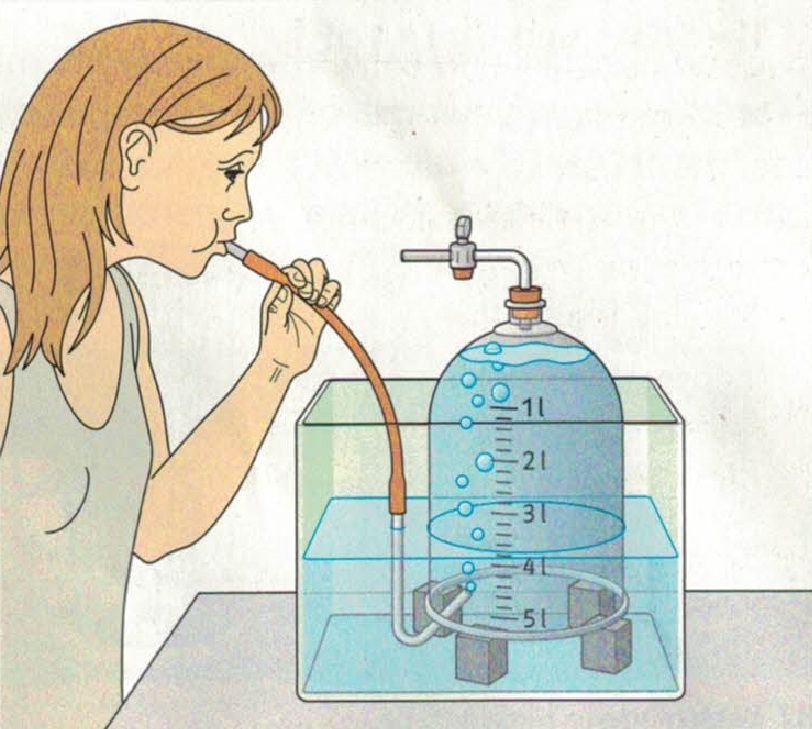
Homepage WebSites Unterrichtsstunden Physik 7./8. Klasse