Kapitel 1 : Körper und Stoffe
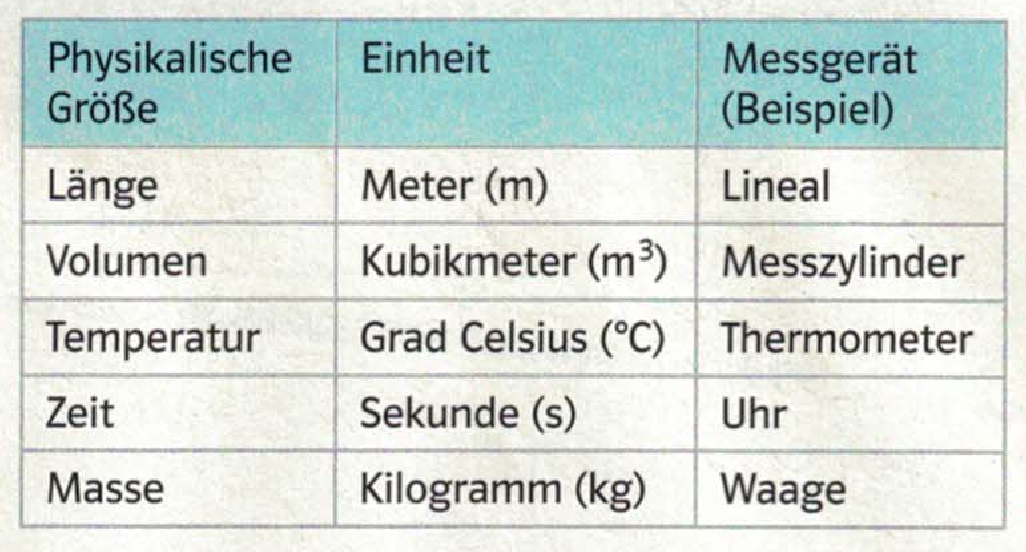
1.1 Messung physikalischer Grössen
1.2 Beschreibung von Körpern
1.3 Masse
1.4 Dichte von Stoffen
1.2 Das magnetische Feld
Quellen
Schmöger, Stötzer: "Impulse Physik Klasse 7/8" [ISBN: 978-3-12-772542-1]Klett Verlag : Impulse Physik 7/8
Wikipedia : Observable
Wikipedia : Messung
GeoGebra : Fläche Kreis
StudiFlix : Volumen Quader / Würfel
1.1 Messung physikalischer Grössen
Physikalische Messgrösse: Observable
Beispiel: Länge $L$$L = 5 \cdot m = 5 m$ (1) "Die Länge $L$ beträgt $5$ Meter"
Beispiel: Zeit $T$
$T = 1.2 \cdot s = 1.2 s$ (2) "Die Zeit $T$ beträgt $1.2$ Sekunden"
Beispiel: Geschwindigkeit $V$ als (zurückgelegter) Weg $L$ geteilt durch (die benötigte) Zeit $T$
$V = \dfrac{L}{T} = \dfrac{5 \cdot m}{1.2 \cdot s} = \dfrac{5}{1.2} \cdot \dfrac{m}{s} = 4.17 \dfrac{m}{s}$ (3) "Die Geschwindigkeit $V$ beträgt $4.17$ Meter pro Sekunde"
Frage: Was ist eine physikalische Messgrösse?
Definition: Eine physikalische Messgrösse $M$(Measurement) beinhaltet:
• einen Wert $V$(Value) und
• eine Einheit $U$(Unit):
$\boxed{M = V \cdot U = VU}$ (4)
• Wert $V$ und Einheit $U$ sind immer miteinander multiplikativ verknüpft.
In Kurzschreibweise kann der Malpunkt "$\cdot$" auch weggelassen werden:
$\Rightarrow M = V \cdot U = VU$
• Einheitsoperator $[..]$ zur Berechnung der Einheit $U$ aus der Observablen $M$:
$\boxed{[M] = [V \cdot U] = [V] \cdot [U] = 1 \cdot U = U}$ (5)
Definition: Observable
Eine "physikalische Messgrösse" nennen wir "Observable".
$\boxed{O := M = V \cdot U = VU}$ (6) : Definition Observable
Eine Observable besteht aus dem Produkt ihres Wertes $V$ und ihrer Einheit $U$.
$\boxed{[O] = [M] = [V \cdot U] = U}$ (7) : Einheit Observable
Eine Einheit einer Observablen $U$ berechnet sich durch den Einheitsoperator $[..]$ angewandt auf $O$.
Rechnen mit Observablen
Wert und Einheit
Physikalische Messgrösse Geschwindigkeit: $v$Definitionsgleichung:
Geschwindigkeit: $\boxed{v := \dfrac{s}{t}}$ (11) mit $\boxed{[v] = \dfrac{m}{s}}$ (12)
zurückgelegte Strecke: $s$ mit $[s] = m$
benötigte Zeit: $t$ mit $[t] = s$
Beispiel: siehe (1), (2), (3)
WICHTIGE FOLGERUNG: Geschwindigkeiten werden mit einem Wert und einer
Einheit $[\dfrac{weg}{zeit}]$ Meter pro Sekunde oder Kilometer pro Stunde angegeben -
Niemals "Stundenkilometer" verwenden, da die Einheit $[zeit \cdot weg] = h \cdot km$
keiner sinnvollen physikalischen Messgrösse entspricht!
Umrechung von Einheiten
Umrechung: Meter $\leftarrow \rightarrow$ Kilometer$\boxed{1 km = 1000 m~}$ (21)
$\boxed{1 m = 0.001 km}$ (22)
Umrechung: Sekunde $\leftarrow \rightarrow$ Minute $\leftarrow \rightarrow$ Stunde
$\boxed{1 h = 60 m = 3600 s~~}$ (23) $m$ bedeutet hier Minuten, nicht Meter!
$\boxed{\dfrac{1}{60} h = 1 m = 60 s~~~~~}$ (24)
$\boxed{\dfrac{1}{3600} h = \dfrac{1}{60} m = 1 s}$ (25)
Umrechung: Meter pro Sekunde $\leftarrow \rightarrow$ Kilometer pro Stunde
Ansatz:
$1 \dfrac{m}{s} = 1 \dfrac{m}{s} ~~\big\vert$ rechte Seite auf $\dfrac{km}{h}$ erweitern
Meter umrechnen in Kilometer: $1 km = 1000 m \rightarrow 1m = \dfrac{1}{1000} km = \dfrac{km}{1000}$
Sekunden umrechnen in Stunden: $1 h = 3600 s \rightarrow 1s = \dfrac{1}{3600} h = \dfrac{h}{3600}$
$1 \dfrac{m}{s} = \dfrac{1 m}{1 s} = \dfrac{1 km}{1000} \cdot \dfrac{3600}{1 h} = \dfrac{km}{1000} \cdot \dfrac{3600}{h} = \dfrac{3600}{1000} \cdot \dfrac{km}{h} = 3.6 \dfrac{km}{h}$
Umrechung Meter pro Sekunde in Kilometer pro Stunde:
$\boxed{1 \dfrac{m}{s} = 3.6 \dfrac{km}{h}}$ (26)
Umstellen der Gleichung (2) führt zur Umrechnung von $\dfrac{km}{h}$ nach $\dfrac{m}{s}$ :
Umrechung Kilometer pro Stunde nach Meter pro Sekunde:
$\boxed{1 \dfrac{km}{h} = \dfrac{1}{3.6} \dfrac{m}{s}}$ (27)
Beispiel: $v = 30 \dfrac{km}{h}$ in $\dfrac{m}{s}$ umrechnen
$v = 30 \dfrac{km}{h} = 30 \dfrac{1000m}{3600s} = \dfrac{30 \cdot 1000}{3600} \dfrac{m}{s} = \dfrac{300}{36} \dfrac{m}{s}$ $\Rightarrow \boxed{v = 8.33 \dfrac{m}{s}}$ (28)
Beispiel: $v = 100 \dfrac{m}{s}$ in $\dfrac{km}{h}$ umrechnen
$v = 100 \dfrac{m}{s} = 100 \cdot 3.6 \dfrac{km}{h} = 360 \dfrac{km}{h}$ $\Rightarrow \boxed{v = 360 \dfrac{km}{h}}$ (29)
Die Messung
Definition: MessungWikipedia: "Eine Messung ist der experimentelle Vorgang, durch den ein spezieller Wert einer physikalischen Grösse als Vielfaches einer Einheit oder eines Bezugswertes ermittelt wird."
Beispiel: Wieviele Tüten Milch passen in einen Milchtankwagen?


Ergebnis: $\boxed{I_{tankinhalt} = 12345 \cdot tueten = 12345 ~ tueten}$ (30)
Messung einer Länge






Die Observable Länge $L$ wird in der Grundeinheit Meter $m$ gemessen.
Für die Länge $L$ einer Geraden gilt: $\boxed{L_{gerade} = a}$ (31)
Längenmessung von $a$ ergibt: $\boxed{a=2.5m}$ (32)
Berechnung der Länge $L$:
$L = a = 2.5 \cdot m = 2.5m$
Ergebnis:
Bei der gemessenen Länge $a=2.5$ einer Geraden beträgt die
Gesamtlänge dieser Gerade (trivialerweise) $\boxed{L_{gerade} = 2.5m}$. (33)
Wichtig:
Die hier abgebildeten Längenmesser messen direkt und ausschliesslich gerade Weglängen!
Weglägen mit Krümmungen sind nur indirekt messbar!
Messung einer Fläche

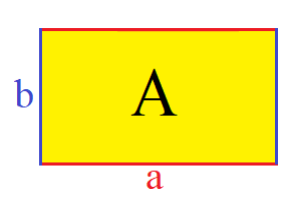
Die Observable Fläche $A$ wird in Quadratmetern $m^2$ gemessen.
Messvorschrift: Fläche Rechteck
Speziell für die Fläche $A$ eines Rechtecks gilt: $\boxed{A_{rechteck} = a \cdot b}$ (21)
Längenmessung der Seite $a$ ergibt: $\boxed{a=1.20m}$ (22)
Längenmessung der Seite $b$ ergibt: $\boxed{b=0.80m}$ (23)
Berechnung der Fläche $A_{rechteck}$:
$A_{rechteck} = a \cdot b = 1.20 \cdot m \cdot 0.80 \cdot m = 0.96 \cdot m \cdot m = 0.96m^2$
Ergebnis:
Bei den Seitenlängen $a=1.20m$ und $b=0.80m$
eines Rechtecks beträgt die Fläche $\boxed{A_{rechteck} = 0.96m^2}$. (24)
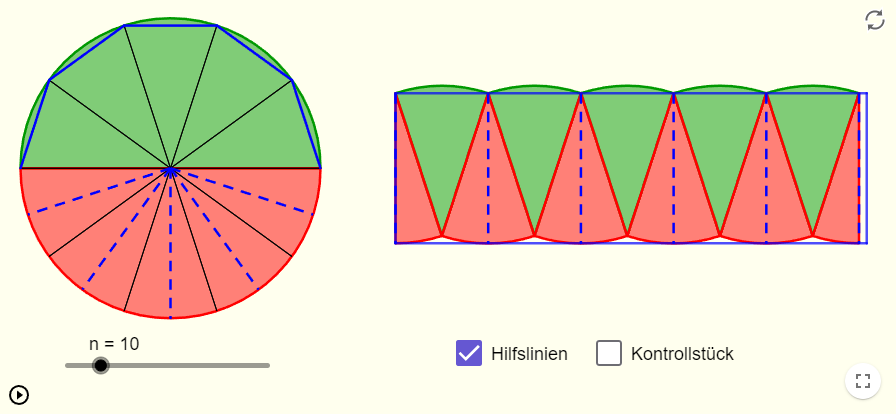
Messvorschrift: Fläche Kreis
Speziell für die Fläche $A$ eines Kreises gilt: $\boxed{A_{kreis} = \pi \cdot r^2}$ (25)
Längenmessung des Radius $r$ ergibt: $\boxed{r=1m}$ (26)
Berechnung der Fläche $A_{kreis}$:
$A_{kreis} = \pi \cdot r^2 = 3.14159 \cdot (1 \cdot m)^2 = 3.142 m^2 =$
Ergebnis:
Mit dem Radius $r=1m$ eines Kreises beträgt seine Fläche $\boxed{A_{kreis} = 3.142 m^2}$. (27)
Messung eines Volumens
Die Observable Volumen $V$ wird in Kubikmetern $m^3$ gemessen.
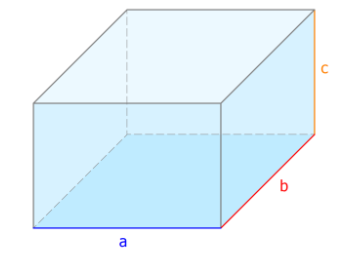
Volumen eines Quaders
Speziell für das Volumen $V$ eines Quaders gilt: $\boxed{V_{quader} = a \cdot b \cdot c}$ (31)
Längenmessung von $a$ ergibt: $\boxed{a=5.10cm}$ (32)
Längenmessung von $b$ ergibt: $\boxed{b=2.90cm}$ (33)
Längenmessung von $c$ ergibt: $\boxed{c=1.05cm}$ (34)
Berechnung des Volumens $V_{quader}$:
$V_{quader} = a \cdot b \cdot c = 5.10cm \cdot 2.90cm \cdot 1.05cm = 15.53cm^3$
Ergebnis:
Bei den Seitenlängen $a=5.10cm$ , $b=2.90cm$ und $c=1.05cm$
eines Quaders beträgt das Volumen $\boxed{V_{quader} = 15.53cm^3}$. (35)
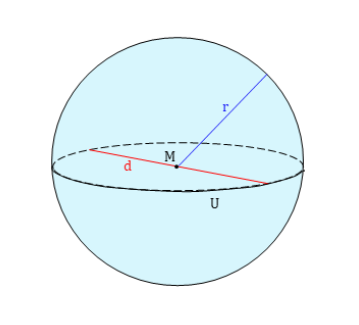
Volumen einer Kugel
Speziell für das Volumen $V$ einer Kugel gilt: $\boxed{V_{kugel} = \dfrac{4}{3} \cdot \pi \cdot r^3}$ (36)
Längenmessung des Radius $r$ ergibt: $\boxed{r=5cm}$ (37)
Berechnung des Volumens $V_{kugel}$:
$V_{kugel} = \dfrac{4}{3} \cdot \pi \cdot r^3 = \dfrac{4}{3} \cdot \pi \cdot (5cm)^3 = \dfrac{4}{3} \cdot \pi \cdot 125cm^3 = 523.6 cm^3$
Ergebnis:
Bei einem Radius $r=5cm$ ergibt sich das Volumen einer Kugel zu: $\boxed{V_{kugel} = 523.6cm^3}$. (38)
Messung einer Masse





Die Observable Masse $M$ wird in der Grundeinheit Kilogramm $kg$ gemessen.
Massenbestimmung mit mechanischer Tischwaage: $\boxed{M_{kohl} = 1.24 kg}$ (41)
Massenbestimmung mit elektronischer Tischwaage: $\boxed{M_{eichgewicht} = 30.00 kg}$ (42)
Messung der Zeit





Die Observable Zeit $T$ wird in der Grundeinheit Sekunden $s$ gemessen.
Von Stoppuhren kann die verstrichene Zeit $T$ in Sekunden direkt abgelesen werden.
Zeitmessung mit einer mechanischen Stoppuhr: $\boxed{T_{stoppuhr} = 10.0 s}$ (51)
Zeitmessung mit einer digitalen Uhr:
$\boxed{T_{uhr} = 11h 52m 25s = 11 \cdot 60 \cdot 60 s + 52 \cdot 60 s + 25 s = 42745 s}$ (52)
Homepage WebSites Unterrichtsstunden Physik 7./8. Klasse