Fallgesetze - Waagerechter Wurf
Übersicht
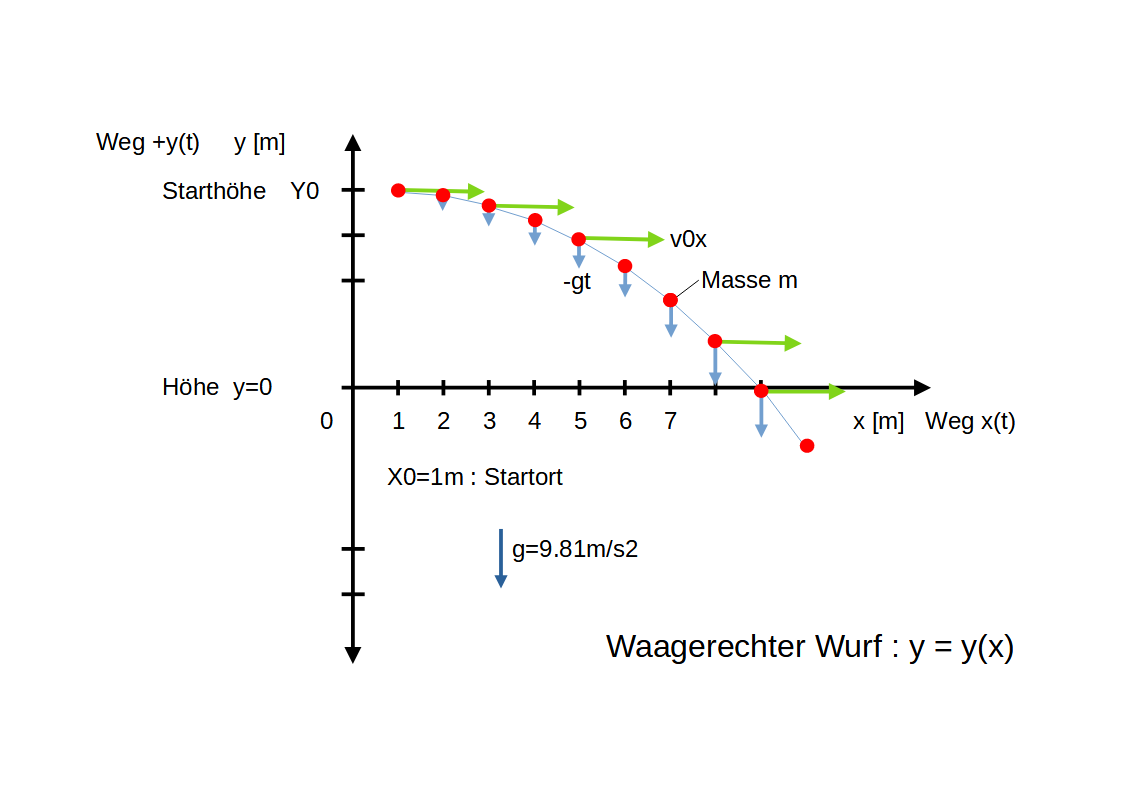
• Masse $m$ wird mit der Anfangsgeschwindigkeit $v_{0x}$ in positive X-Richtung geworfen.
• Die Bewegung findet in der X/Y-Ebene statt.
• Während des Fluges wirkt die Erdbeschleunigung $g$ auf die Masse $m$ und erzeugt eine
Geschwindigkeits- und damit eine Orts-Komponente in negativer $y$-Richtung.
• Masse $m$, Erdbeschleunigung $g$ und Anfangsgeschwindigkeit $v_{0x}$ sind zeitlich konstant.
• Frei wählbarer Anfangsort $(x_0, y_0)$ für den Abwurf mit Anfangsgeschwindigkeit $v_{0x}$ frei wählbar.
• Beide Bewegungen in $X$ und $Y$ sind nach dem SuperPositionsPrinzip voneinander unabhängig.
(SPP - SuperPositionsPrinzip).
Weg-Zeit-Funktionen $x(t), y(t)$ des Senkrechten Wurfs:
$\boxed{x(t) = v_{0x}t + x_0}$ (1)
$\boxed{y(t) = y_0 - \dfrac{gt^2}{2}}$ (2)
Geschwindigkeit-Zeit-Funktionen $v_x(t), v_y(t)$ des Senkrechten Wurfs:
$\boxed{v_x = v_{0x} = const}$ (3)
$\boxed{v_y = v_{gy} = -gt}$ (4)
Wurfweite $x_w$ :
$\boxed{x_w = x_0 + v_{0x} \sqrt{\dfrac{2 y_0}{g}}}$ (7)
Wurfdauer $t_d$ :
$\boxed{t_d = \dfrac{x_w - x_0}{v_{0x}}}$ (8)
Aufprallgeschwindigkeit $v_p$ :
$\boxed{v_p = \sqrt{v_{0x}^2 + \dfrac{g^2}{v_{0x}^2} [x_w - x_0]^2}}$ (9)
Bahnkurve $y = y(x)$ :
$\boxed{y(x) = y_0 - \dfrac{g [x - x_0]^2}{2 {v_{0x}^2}}}$ (10)
Download
• Download dieser Seite als Pdf-Dokument: WaagerechterWurf.pdf• Download des Python-Programms: WaagerechterWurf.py
Herleitung
Geschwindigkeiten:Abwurf-Geschwindigkeit in positiver $x$-Richtung
$\boxed{v_x = v_{0x} = const}$ (3)
Fallgeschwindigkeit in negativer $y$-Richtung
$\boxed{v_y = v_{gy} = -gt}$ (4)
Ortsfunktionen durch Integration (mit Integrationskonstanten):
$x(t) = \int\limits_t{v_{0x} dt}$
$\boxed{x(t) = v_{0x}t + x_0}$ (1)
$y(t) = \int\limits_t{(-gt) dt}$
$\boxed{y(t) = y_0 - \dfrac{gt^2}{2}}$ (2)
Die Bewegungskurve $y = y(x)$ muss aus beiden Gleichungen (1) und (2) $t$ eleminiert werden:
$x = v_{0x}t + x_0$
$x - x_0 = v_{0x}t$
$\boxed{t = \dfrac{x - x_0}{v_{0x}}}$ (5)
$y - y_0 = - \dfrac{gt^2}{2}$
$y - y_0 = - \dfrac{g[\dfrac{x - x_0}{v_{0x}}]^2}{2}$
$y - y_0 = - \dfrac{g(x - x_0)^2}{2 v_{0x}^2}$
$\boxed{y(x) = - \dfrac{g}{2 v_{0x}^2}(x - x_0)^2 + y_0}$ (6)
Damit folgt aus der Bahnkurve $0y=y(x)$ des Waagerechten Wurfs in Gleichung (6) eine
halbe nach unten geöffnete Parabel.
Die Integrationskonstanten x0 und y0 geben die Verschiebung des Scheitelpunkts der Parabel
vom Koordinaten-Ursprung an.
Weitere Berechnungen
Wurfweite
Bedingung: $y(x_w) = 0$ in (6) einsetzen:$y(x_w) = 0 = - \dfrac{g}{2 v_{0x}^2}(x_w - x_0)^2 + y_0$
$y_0 = \dfrac{g}{2 v_{0x}^2}(x_w - x_0)^2 $
$(x_w - x_0)^2 = \dfrac{2 y_0 v_{0x}^2}{g}$
$x_w - x_0 = v_{0x} \sqrt{\dfrac{2 y_0}{g}}$
$\boxed{x_w = x_0 + v_{0x} \sqrt{\dfrac{2 y_0}{g}}}$ (7)
($y_0 > 0$ : muss für die Existenz einer Wurfweite gegeben sein!)
Wurfdauer
Wurfweite $x_w$ in Gleichung (5) einsetzen:$\boxed{t_w = \dfrac{x_w - x_0}{v_{0x}}}$ (8)
Aufprallgeschwindigkeit
Geschwindigkeit in $x$-Richtung:$v_x = v_{0x} = const$ (3)
Geschwindigkeit in $y$-Richtung:
$v_y(t_w) = -g t_w$ (4)
Aufprallgeschwindigkeit aus Superpositionsprinzip der Geschwindigkeiten:
$v_p = \sqrt{v_x^2 + v_y^2(t_w)}$
$v_p = \sqrt{v_{0x}^2 + g^2 t_w^2}$
Mit Gleichung (8) folgt:
$v_p = \sqrt{v_{0x}^2 + g^2 [\dfrac{x_w - x_0}{v_{0x}}]^2}$
$\boxed{v_p = \sqrt{v_{0x}^2 + \dfrac{g^2}{v_{0x}^2} [x_w - x_0]^2}}$ (9)
Darstellung der Gleichungen mit Python
Sehen wir uns nun all diese Gleichungen in einem darstellenden Python Programm an: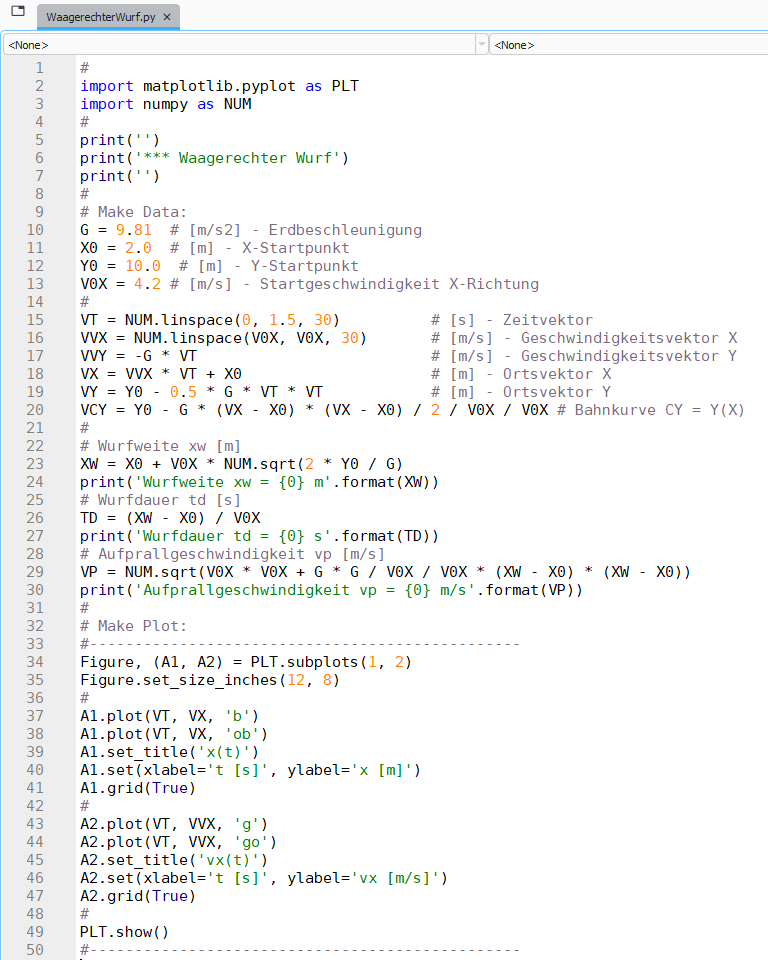
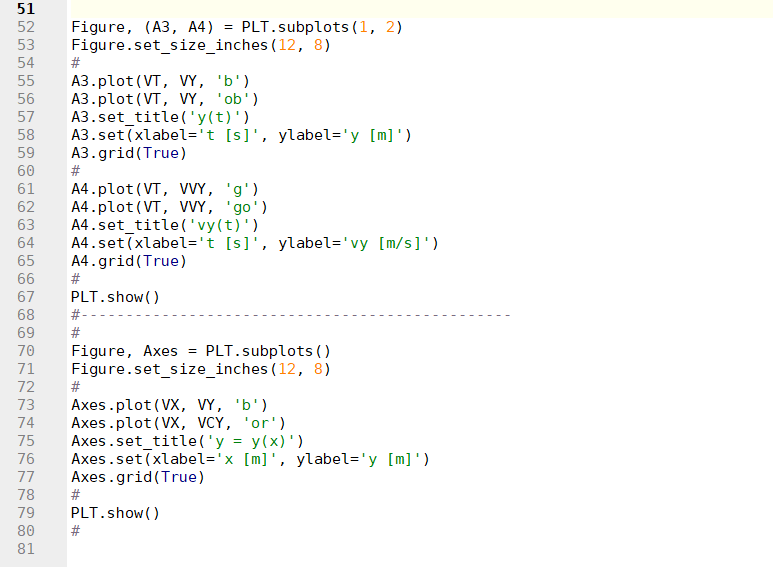
Download des Python-Programms: WaagerechterWurf.py
Das Python-Programm WaagerechterWurf startet mit der Einbindung zweier Bibliotheken:
einer Plot-Bibliothek mit Namen PLT und einer Numerischen Bibliothek mit Namen NUM.
Danach erfolgt die Ausgabe des Programm-Headers "WaagerechterWurf".
Im folgenden Abschnitt "Make Data" werden alle Daten definiert und erzeugt.
• die Erdbeschleunigung G mit $9.81 \dfrac{m}{s^2}$
• der Abwurfort X0 mit $2m$
• die Anfangshöhe Y0 mit $10m$.
• und die Anfangsgeschwindigkeit V0X mit $4.2 \dfrac{m}{s}$.
Es folgt die Erzeugung eines Vektors VT über die Zeit von $0s$ bis $1.5s$ in $30$ Schritten.
Mit diesem Zeitvektor berechnet sich ein Geschwindigkeitsvektor VVX, ein Geschwindkeitsvektor VVY,
und die beiden Ortsvektoren VX und VY.
Danach finden wir die Gleichungen für die Wurfweite XW, die Waurfdauer TD und
die Aufprallgeschwindigkeit VP.
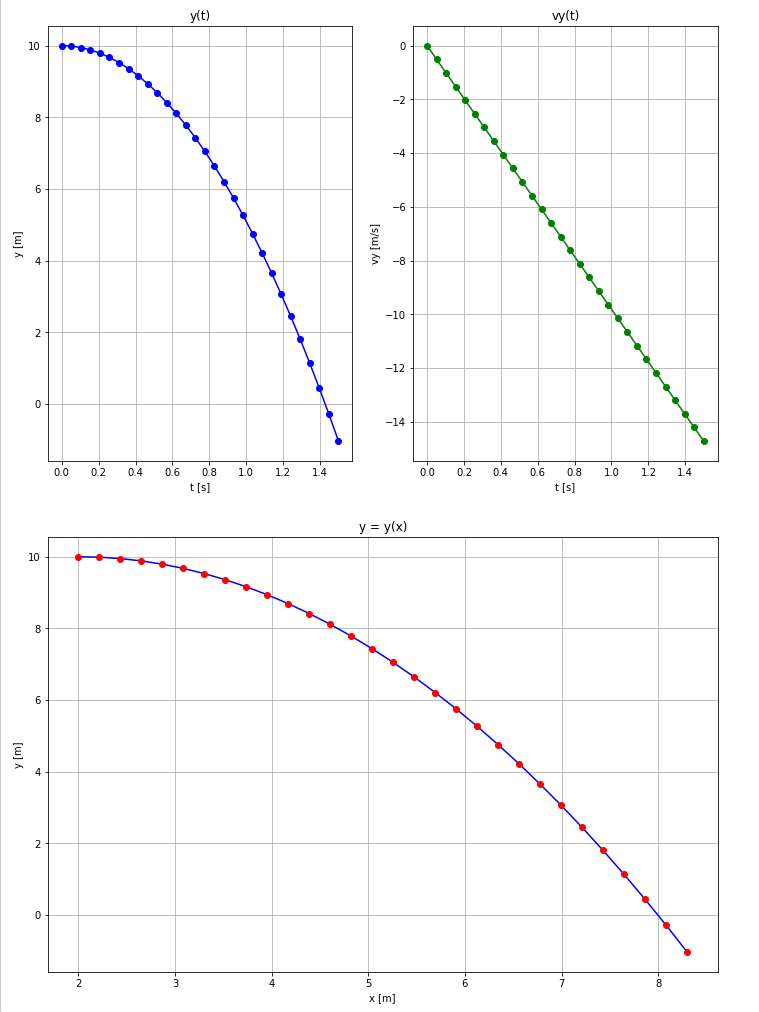
Mit diesen Daten werden im nächsten Abschnitt "Make Plot" zwei Orts-Zeit-Plot $x(t)$ und
$y(t)$ gegen $t$ und zwei Geschwindigkeits-Zeit-Plot $vx(t)$ und $vy(t)$ gegen $t$ berechnet
und ausgegeben.
Im fünften Plot werden die Vektoren der Orts-Zeit-Funktionen mit den Vektoren der Bahnkurve
verglichen.
"Run" zeigt das Ergebnis der berechneten Waagerechter-Wurf-Parameter und die fünf Plots
$x(t)$, $y(t)$, $vx(t)$, $vy(t)$ und $y=y(x)$.
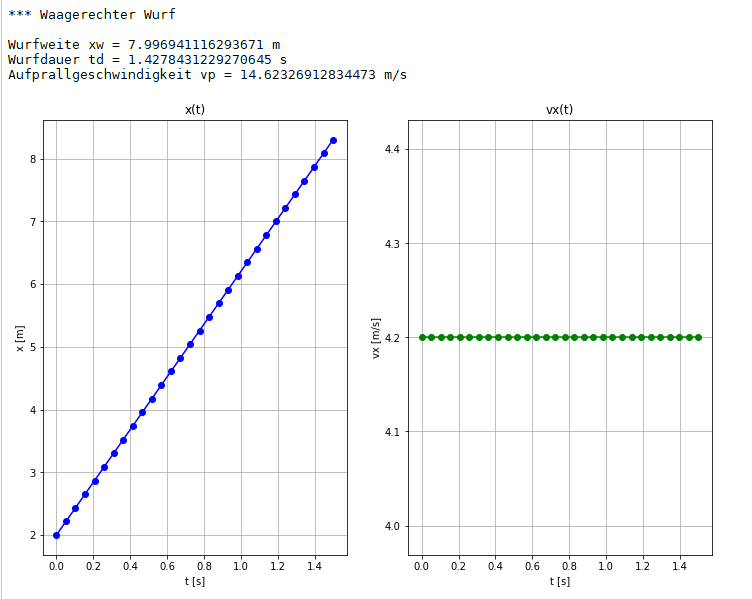
Die berechnete Wurfweite XW von 8 Metern stimmt mit dem Bahnkurvenplot überein.
Ebenso passt die Wurfdauer von 1.4s zu der erreichten Wurfweite von 8m.
Weiterhin ergeben die vx(t) und vy(t)- Plots über Pythagoras eine Aufprallgeschwindigkeit vp von 14.6m/s.
Ausgabe nach dem Start des Python-Programms:
WebSites Module