Fallgesetze - Schiefer Wurf
Übersicht
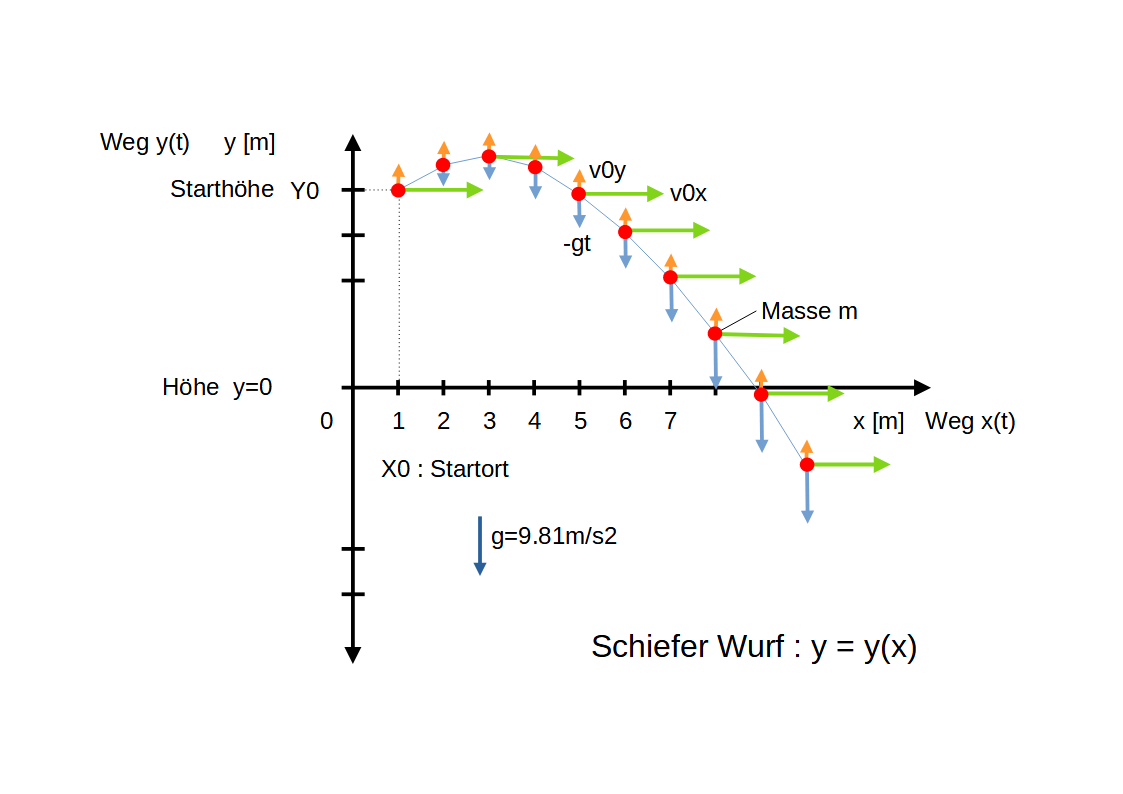
• Die Masse $m$ wird mit der Anfangsgeschwindigkeit $v_0$ unter dem Anfangswinkel $\psi$
in der $X/Y$-Ebene geworfen.
• Während des Fluges wirkt die Erdbeschleunigung $g$ auf die Masse $m$.
• Masse $m$, Erdbeschleunigung $g$ und Anfangsgeschwindigkeit $\vec{v}_0 = (v_{0x},v_{0y})$ sind konstant.
• $\vec{v}_0 = (v_{0x}, v_{0y})$ : Geschwindigkeitskomponenten in $X/Y$-Richtung
• Beide Bewegungen in $X$ und $Y$ sind voneinander unabhängig (SPP - SuperPositionsPrinzip).
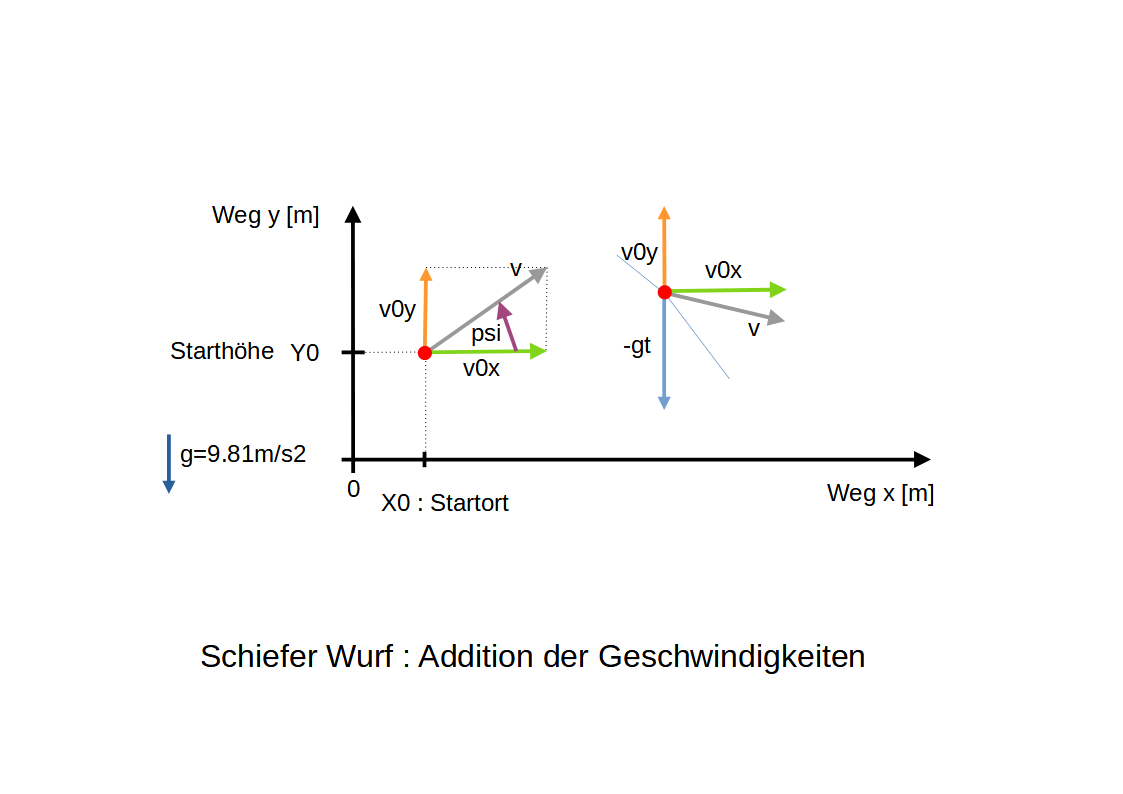
Die Addition der Geschwindigkeiten erfolgt nach der Vektor-Addition der Geschwindigkeiten:
$\boxed{v_x(t) = v(t) \cdot \cos(\psi)}$ (17)
$\boxed{v_y(t) = v(t) \cdot \sin(\psi)}$ (18)
$\boxed{v(t) = \sqrt{v_x(t)^2 + v_y(t)^2}}$ (19)
Weg-Zeit-Funktionen $x(t), y(t)$ des Schiefen Wurfs:
$\boxed{x(t) = v_{0x} t + x_0}$ (5)
$\boxed{y(t) = v_{0y} t -\dfrac{g t^2}{2} + y_0}$ (6)
Geschwindigkeit-Zeit-Funktionen $v_x(t), v_y(t)$ des Schiefen Wurfs:
$\boxed{v_x(t) = v_{0x}}$ (3)
$\boxed{v_y(t) = -gt + v_{0y}}$ (4)
Steigzeit $t_s$ :
$\boxed{t_s = \dfrac{v_{0y}}{g}}$ (7)
Wurfhöhe $y_h$ :
$\boxed{y_h = \dfrac{v_{0y}^2}{2g} + y_0}$ (8)
Wurfzeit $t_w$ :
$\boxed{t_w = \dfrac{v_{0y}}{g} \pm \sqrt{\dfrac{v_{0y}^2}{g^2} + \dfrac{2y_0}{g}}}$ (9)
Wurfweite $x_w$ :
$\boxed{x_w = x_0 + \dfrac{v_{0x} v_{0y}}{g} + v_{0x} \sqrt{\dfrac{v_{0y}^2}{g^2} + \dfrac{2y_0}{g}}}$ (10)
Bahnkurve $y = y(x)$ :
$\boxed{y = y_0 + (x - x_0)\dfrac{v_{0y}}{v_{0x}} -\dfrac{g}{2 v^2_{0x}} [ x - x_0]^2}$ (12)
Aufprallgeschwindigkeit $v_p$ (mit Wurfzeit $t_w$):
$\boxed{v_p = \sqrt{v_{0x}^2 + [v_{0y} - g t_w]^2}}$ (16)
Download
• Download dieser Seite als Pdf-Dokument: SchieferWurf.pdf• Download des Python-Programms: SchieferWurf.py
Herleitung
Analog zum freien Fall und mit dem SPP gelten die Bewegungsgleichungen:$\boxed{v_x(t) = v_{0x}}$ (1)
$\boxed{v_y(t) = -gt + v_{0y}}$ (2)
mit
$\boxed{v_{0x} = v_0 \cos(\phi)}$ (3)
$\boxed{v_{0y} = v_0 \sin(\phi)}$ (4)
Integration beider Funktion (1) und (2) über die Zeit ergibt:
$\boxed{x(t) = v_{0x} t + x_0}$ (5)
$\boxed{y(t) = v_{0y} t -\dfrac{g t^2}{2} + y_0}$ (6)
mit den wählbaren Integrationskonstanten $x_0$ und $y_0$ (Anfangsort).
Weitere Berechnungen
Steigzeit
Bedingung mit (2):$v_y(t_s) = 0 = -gt_s + v_{0y}$
$gt_s = v_{0y}$
$\boxed{t_s = \dfrac{v_{0y}}{g}}$ (7)
Wurfhöhe
Steigzeit (7) in (6) einsetzen:$y_h(t_s) = v_{0y} t_s -\dfrac{g t_s^2}{2} + y_0$
$y_h = v_{0y} [\dfrac{v_{0y}}{g}] -\dfrac{g [\dfrac{v_{0y}}{g}]^2}{2} + y_0$
$y_h = \dfrac{v_{0y}^2}{g} - g \dfrac{v_{0y}^2}{2g^2} + y_0$
$y_h = \dfrac{v_{0y}^2}{g} - \dfrac{v_{0y}^2}{2g} + y_0$
$\boxed{y_h = y_0 + \dfrac{v_{0y}^2}{2g}}$ (8)
Wurfzeit
Bedingung: (6) identisch Null$y(t_w) = 0 = v_{0y} t_w -\dfrac{g t_w^2}{2} + y_0$
$0 = v_{0y} t_w -\dfrac{g t_w^2}{2} + y_0$
$0 = t_w^2 -2\dfrac{v_{0y}}{g} t_w -\dfrac{2y_0}{g}$
$P := \dfrac{v_{0y}}{g}$ und $Q := \dfrac{2y_0}{g}$
$0 = t_w^2 - 2 P t_w - Q$
Quadratische Ergänzung:
$0 = t_w^2 - 2 P t_w + P^2 - P^2 - Q$
$0 = [t_w - P]^2 - P^2 - Q$
$[t_w - P]^2 = P^2 + Q$
$t_w = P \pm \sqrt{P^2 + Q}$
Zurück-einsetzen $P, Q$ :
$t_w = \dfrac{v_{0y}}{g} \pm \sqrt{[\dfrac{v_{0y}}{g}]^2 + \dfrac{2y_0}{g}}$
$\boxed{t_w = \dfrac{v_{0y}}{g} \pm \sqrt{\dfrac{v_{0y}^2}{g^2} + \dfrac{2y_0}{g}}}$ (9)
Die Wurfzeit $t_w$ hängt damit nur von der $Y$-Bewegung ab.
Wurfweite
Bedingung: Wurfzeit $t_w$ (9) in $x(t)$ (5) einsetzen$x(t_w) = x_w = v_{0x} t_w + x_0$
$x_w = v_{0x} [\dfrac{v_{0y}}{g} \pm \sqrt{\dfrac{v_{0y}^2}{g^2} + \dfrac{2y_0}{g}}] + x_0$
$\boxed{x_w = x_0 + \dfrac{v_{0x} v_{0y}}{g} + v_{0x} \sqrt{\dfrac{v_{0y}^2}{g^2} + \dfrac{2y_0}{g}}}$ (10)
Bahnkurve
Die Bahnkurve $y = y(x)$ ergibt sich aus der Elemination von $t$ in (5) und (6):Aus (5) folgt:
$x = v_{0x} t + x_0$
$\boxed{t = \dfrac{x}{v_{0x}} - \dfrac{x_0}{v_{0x}}}$ (11)
$t$ einsetzen in (6)
$y(t) = v_{0y} t -\dfrac{g t^2}{2} + y_0$
ergibt:
$y = v_{0y}[ \dfrac{x}{v_{0x}} - \dfrac{x_0}{v_{0x}}] -\dfrac{g [ \dfrac{x}{v_{0x}} - \dfrac{x_0}{v_{0x}}]^2}{2} + y_0$
$y = \dfrac{x v_{0y}}{v_{0x}} - \dfrac{x_0 v_{0y}}{v_{0x}} -\dfrac{g}{2 v^2_{0x}} [ x - x_0]^2 + y_0$
$\boxed{y = y_0 -\dfrac{g}{2 v^2_{0x}} [ x - x_0]^2 + (x - x_0)\dfrac{v_{0y}}{v_{0x}}}$ (12)
Die Bahnkurve $y = y(x)$ zeigt sich als eine nach unten geöffnete und verschobene Parabel mit Abwurfpunkt $(x_0, y_0)$.
Alternative Berechnung der Wurfweite
Die Wurfweite $x_w$ wird nach Abwurf am Punkt $(x_0, y_0)$ am Schnittpunkt der Bahnkurve mit der $X$-Achse erreicht.Bedingung mit (12) $y := 0$ für die Wurfweite $x_w$:
$y = 0 = y_0 + (x_w - x_0)\dfrac{v_{0y}}{v_{0x}} -\dfrac{g}{2 v^2_{0x}} [x_w - x_0]^2$
$0 = y_0 + (x_w - x_0)\dfrac{v_{0y}}{v_{0x}} -\dfrac{g}{2 v^2_{0x}} [x_w^2 - 2 x_w x_0 + x_0^2] \quad \bigg\vert \cdot -\dfrac{2 v^2_{0x}}{g}$
$0 = - \dfrac{2 v^2_{0x}y_0}{g} -(x_w - x_0) \dfrac{2 v_{0x} v_{0y}}{g} + x_w^2 - 2 x_w x_0 + x_0^2$
$0 = x_w^2 - x_w \dfrac{2 v_{0x} v_{0y}}{g} - 2 x_w x_0 + x_0^2 + \dfrac{2 v_{0x} v_{0y} x_0}{g} - \dfrac{2 v^2_{0x}y_0}{g}$
$0 = x_w^2 - 2x_w \bigg[\dfrac{ v_{0x} v_{0y}}{g} + x_0 \bigg] + \bigg[x_0^2 + \dfrac{2 v_{0x}}{g} (v_{0y} x_0 - v_{0x}y_0) \bigg]$
$P := \dfrac{ v_{0x} v_{0y}}{g} + x_0$
$Q := x_0^2 + \dfrac{2 v_{0x}}{g} (v_{0y} x_0 - v_{0x}y_0)$
$0 = x_w^2 - 2 P x_w + Q$
Quadratische Ergänzung:
$0 = x_w^2 - 2 P x_w + P^2 - P^2 + Q$
$0 = (x_w - P)^2 - P^2 + Q$
$(x_w - P)^2 = P^2 - Q$
$x_w - P = \pm \sqrt{P^2 - Q}$
$x_w = P \pm \sqrt{P^2 - Q}$
$P, Q$ zurück eingesetzt:
$x_w = x_0 + \dfrac{ v_{0x} v_{0y}}{g} \pm \sqrt{[\dfrac{v_{0x} v_{0y}}{g} + x_0]^2 - x_0^2 - \dfrac{2 v_{0x}}{g} (v_{0y} x_0 - v_{0x}y_0)}$
$x_w = x_0 + \dfrac{ v_{0x} v_{0y}}{g} \pm \sqrt{\dfrac{v_{0x}^2 v_{0y}^2}{g^2} + x_0^2 + \dfrac{2 v_{0x} v_{0y} x_0}{g}- x_0^2 - \dfrac{2 v_{0x} v_{0y} x_0}{g} + \dfrac{2 v_{0x}^2 y_0}{g}}$
$x_w = x_0 + \dfrac{ v_{0x} v_{0y}}{g} \pm \sqrt{\dfrac{v_{0x}^2 v_{0y}^2}{g^2} + \dfrac{2 v_{0x}^2 y_0}{g}}$
$\boxed{x_w = x_0 + \dfrac{ v_{0x} v_{0y}}{g} \pm v_{0x} \sqrt{\dfrac{v_{0y}^2}{g^2} + \dfrac{2 y_0}{g}}}$ (13)
Damit ist die alternative Wurfweite (13) identisch mit der Wurfweite in (10).
Alternative Berechnung der Wurfhöhe
Gesucht wird das Maximum der Bahnkurve $y = y(x)$ (12):$!max(y = (x - x_0)\dfrac{v_{0y}}{v_{0x}} -\dfrac{g}{2 v^2_{0x}} [ x - x_0]^2 + y_0)$
Erste Ableitung nach $x$ auf Null setzen -> Maximum an der Stelle $x_h$:
$\dfrac{dy}{dx} = \dfrac{d}{dx}\bigg[ (x_h - x_0)\dfrac{v_{0y}}{v_{0x}} -\dfrac{g}{2 v^2_{0x}} [x_h - x_0]^2 + y_0\bigg] = 0$
$0 = \dfrac{v_{0y}}{v_{0x}} -\dfrac{g}{v^2_{0x}} [x_h - x_0]$
$0 = v_{0x} v_{0y} - g [x_h - x_0]$
$g [x_h - x_0] = v_{0x} v_{0y}$
$\boxed{x_h = x_0 + \dfrac{v_{0x} v_{0y}}{g} }$ (14)
Somit ergibt sich $x_h$ als die Stelle mit der maximalen Wurfhöhe.
Beweis für ein Maximum an der Stelle $x_h$: $\quad \dfrac{d^2y}{dx^2} < 0$
$\dfrac{d^2y}{dx_h^2} = \dfrac{dy}{dx_h}\bigg[\dfrac{v_{0y}}{v_{0x}} -\dfrac{g}{v^2_{0x}} [x_h - x_0] \bigg] = -\dfrac{g}{v^2_{0x}} < 0 \quad$ q.e.d.
Damit zeigt die Stelle $x_h$ ein echtes Maximum der Wurfhöhe.
eingesetzt in (5):
$y_h = (x_h - x_0)\dfrac{v_{0y}}{v_{0x}} -\dfrac{g}{2 v^2_{0x}} [ x_h - x_0]^2 + y_0$
$y_h = (x_0 + \dfrac{v_{0x} v_{0y}}{g} - x_0)\dfrac{v_{0y}}{v_{0x}} -\dfrac{g}{2 v^2_{0x}} [ x_0 + \dfrac{v_{0x} v_{0y}}{g} - x_0]^2 + y_0$
$y_h = \dfrac{v_{0x} v_{0y}}{g}\dfrac{v_{0y}}{v_{0x}} -\dfrac{g}{2 v^2_{0x}} [ \dfrac{v_{0x} v_{0y}}{g}]^2 + y_0$
$y_h = \dfrac{v_{0y}^2}{g} -\dfrac{g}{2 v^2_{0x}} \dfrac{v_{0x}^2 v_{0y}^2}{g^2} + y_0$
$y_h = \dfrac{v_{0y}^2}{g} - \dfrac{ v_{0y}^2}{2g} + y_0$
$\boxed{y_h = y_0 + \dfrac{v_{0y}^2}{2g}}$ (15)
An der Maximalstelle $x_h$ (14) wird dann die grösste Wurfhöhe $y_h$ (15) erreicht.
Die Gleichung (15) für die Wurfhöhe ist identisch mit Gleichung (8).
Aufprallgeschwindigkeit
Geschwindigkeit in $x$-Richtung:$v_x(t) = v_{0x}$ (1)
Geschwindigkeit in $y$-Richtung:
$v_y(t) = -gt + v_{0y}$ (2)
Aufprallgeschwindigkeit aus Superpositionsprinzip der Geschwindigkeiten $v_x(t), v_y(t)$ und mit Wurfdauer $t_w$ :
$v_p = \sqrt{v_x^2(t_w) + v_y^2(t_w)}$ (~19)
$v_p = \sqrt{v_{0x}^2 + [-g t_w + v_{0y}]^2}$
Mit der Gleichung (9) für die Wurfzeit
$\boxed{t_w = \dfrac{v_{0y}}{g} \pm \sqrt{\dfrac{v_{0y}^2}{g^2} + \dfrac{2y_0}{g}}}$ (9)
folgt:
$\boxed{v_p = \sqrt{v_{0x}^2 + [v_{0y} - g t_w]^2}}$ (16)
Darstellung der Gleichungen mit Python
Sehen wir uns nun all diese Gleichungen in einem darstellenden Python Programm an: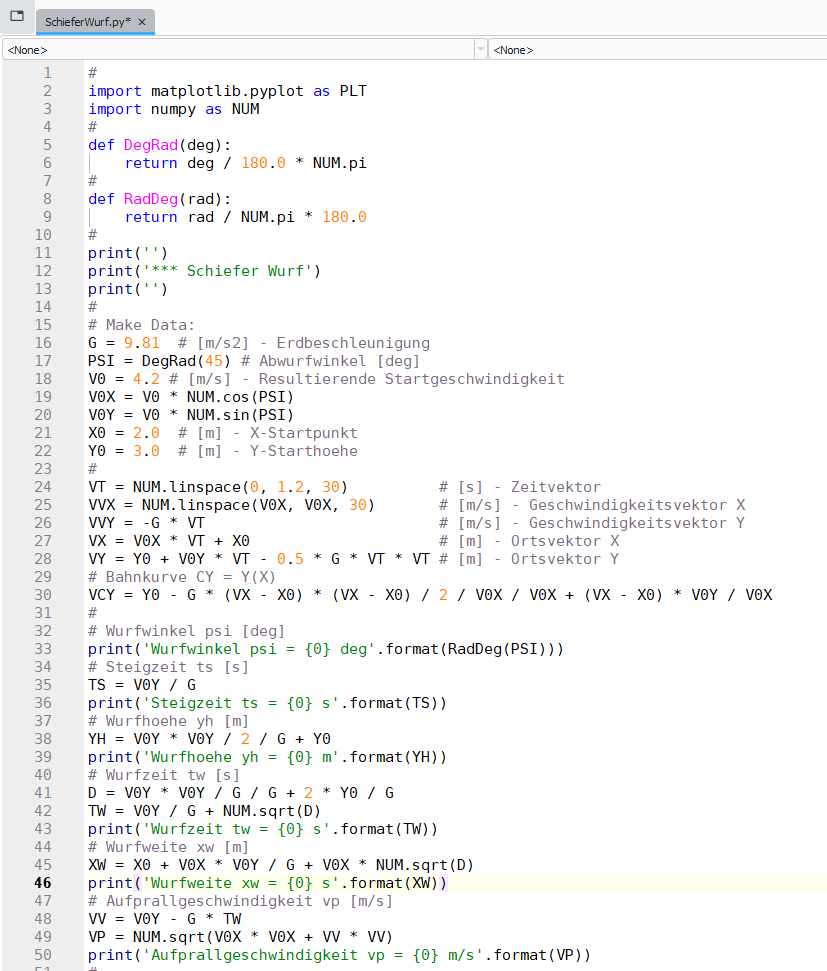
Download des Python-Programms: SchieferWurf.py
Das Python-Programm SchieferWurf startet mit der Einbindung zweier Bibliotheken:
einer Plot-Bibliothek mit Namen PLT und einer Numerischen Bibliothek mit Namen NUM.
Es folgen zwei Hilfsfunktionen DegRad und RadDeg zur Umrechnung von Grad nach Bogenmass.
Danach erfolgt die Ausgabe des Programm-Headers "Schiefer Wurf".
Im folgenden Abschnitt "Make Data" werden alle Daten definiert und erzeugt.
• die Erdbeschleunigung G mit $9.81 \dfrac{m}{s^2}$
• der Abwurfwinkel PSI mit 45 grad,
• die resultierende Startgeschwindigkeit V0 gleich 4.2 m/s,
• die Anteile der Startgeschwindigkeiten in x- und y-Richung V0X und V0Y,
• der Abwurfort X0 mit 2m
• und die Anfangshöhe Y0 mit 3m.
Es folgt die Erzeugung eines Vektors VT über der Zeit von 0s bis 1.2s in 30 Schritten.
Mit diesem Zeitvektor berechnet sich ein Geschwindigkeitsvektor VVX,
ein Geschwindigkeitsvektor VVY und die beiden Ortsvektoren VX und VY.
Eine Form der Bahnkurve bildet der Vektor VCY mit dem Ortsvektor VX.
Anschliessend finden wir die Gleichungen für den Wurfwinkel PSI, die Steigzeit TS,
die Wurfhöhe YH, die Gesamtwurfzeit TW, die Wurfweite XW und die Aufprallgeschwindigkeit VP.
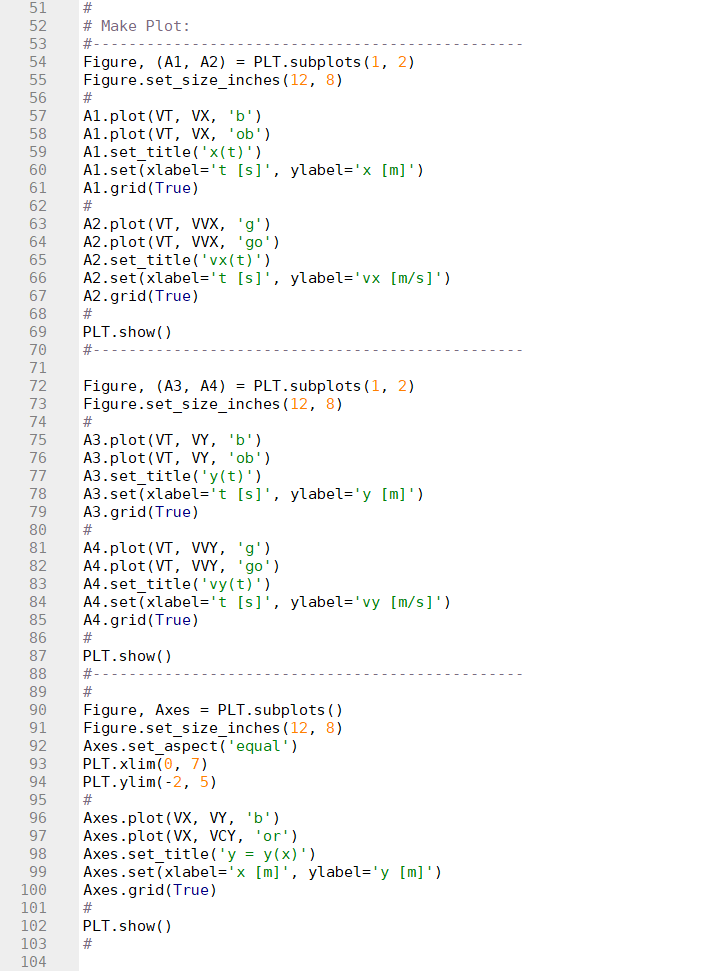
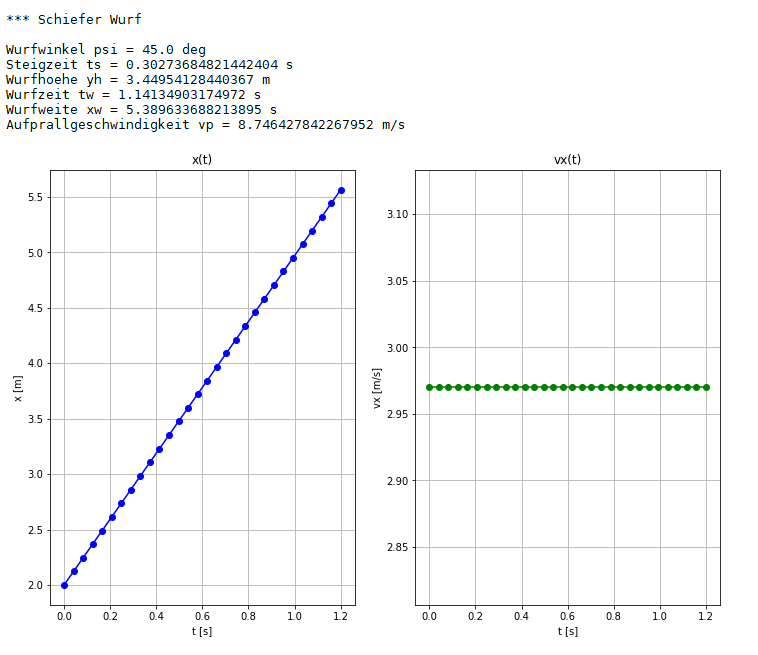
Mit diesen Daten werden im nächsten Abschnitt "Make Plot" zwei Orts-Zeit-Plot $x(t)$ und
$y(t)$ gegen $t$ und zwei Geschwindigkeits-Zeit-Plot $vx(t)$ und $vy(t)$ gegen $t$ berechnet
und ausgegeben.
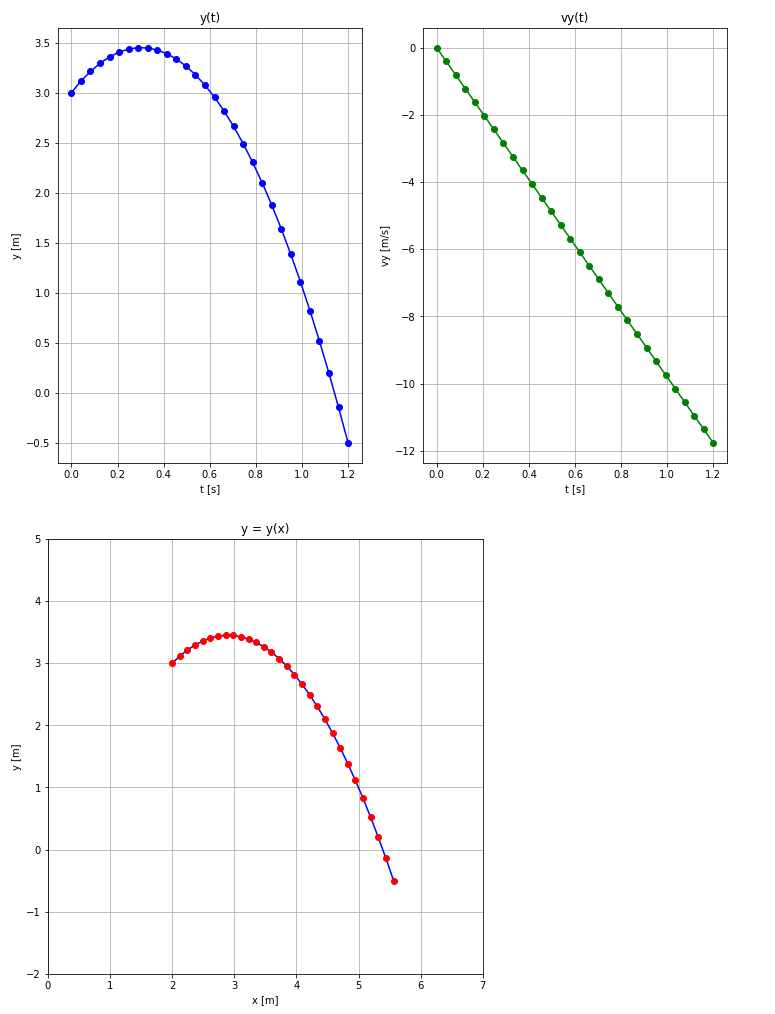
Im fünften Plot werden die Vektoren der Orts-Zeit-Funktionen mit den Vektoren der Bahnkurve
verglichen.
"Run" zeigt das Ergebnis der berechneten Waagerechter-Wurf-Parameter und die fünf Plots
$x(t)$, $y(t)$, $vx(t)$, $vy(t)$ und $y=y(x)$.
Der berechnete Wurfwinkel PSI=45deg stimmt mit Anfangswinkel der Bahnkurve überein.
Die Steigzeit von 0.3s wird durch den y(t)-Plot bestätigt.
Ebenso zeigt der y(t)-Plot die Steighöhe yh von 3.4m.
Die Wurfzeit TW=1.14s passt im y(t)-Plot zur Höhe y=0.
In der Bahnkurve zeigt sich die Wurfweite xw von 5.4m.
Zum Schluss berechnet sich die Aufprallgeschwindigkeit VP zu 9m/s.
Ausgabe nach dem Start des Python-Programms:
WebSites Module