Geodäsie - Entfernung lokaler naher GPS-Punkte

Download Pdf-Dokument: 2205210911_GpsDistance.pdf

Gesucht

Zwischen zwei gegebenen GPS-Ortskoordinaten:

$P_0(\lambda_0, \varphi_0)$ und $P_1(\lambda_1, \varphi_1)$

mit

$\lambda_i$ : geografische Länge, Einheit: $[\lambda_i] = rad$ , $-\pi \leq \lambda_i \leq +\pi$

$\varphi_i$ : geografische Breite, Einheit: $[\varphi] = rad$ , $-\dfrac{\pi}{2} \leq \varphi_i \leq +\dfrac{\pi}{2}$

die Erd-Ellipsoid-Bogen-Entfernungen $dx, dy$ und $ds$
$dx$ mit Einheit: $[dx] = m$ , Strecke in östlicher Richtung positiv und westlicher Richtung negativ
$dy$ mit Einheit: $[dy] = m$ , Strecke in nördlicher Richtung positiv und südlicher Richtung negativ
$ds$ mit Einheit: $[ds] = m$ , positive Strecke in beliebiger Himmelsrichtung
auf der Erdoberfläche linearisiert berechnen.

Quellen

Marlen Schönig: Idee zur Linearisierung des GPS-Entfernungsproblems
Wikipedia: Erdradius
Wikipedia: Earth Radius

Gegeben

sind nun zwei Punkte (im Abstand $ds$ angenähert ohne Krümmung) auf der Erdoberfläche:

$P_0 = (\lambda_0, \varphi_0)$ und $P_1 = (\lambda_1, \varphi_1)$

Gesucht

der Abstand beider Punkte $dx$, $dy$ und $ds$

Lösung

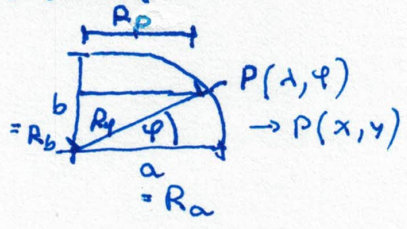
Erdradius am Äquator konstant mit $R_{equator} = 6378137.0 m$ (keine Abhängigkeit vom Längengrad $\lambda$)
Erdradius am Nordpol und Südpol: $R_{pole} = 6356752.314 m$ (identisch für Nord- und Südpol)
Alle anderen Erdradien zwischen Äquator($R_{equator}$) und Polen($R_{pole}$) sind (in erster Näherung) nur abhängig vom Breitengrad $\varphi$ :

$R(\varphi) = \sqrt{\dfrac{[R_{equator}^2 \cos(\varphi)]^2 + [R_{pole}^2 \sin(\varphi)]^2} {[R_{equator} \cos(\varphi)]^2 + [R_{pole} \sin(\varphi)]^2}}$ (1)

weiterhin:
$R_{point}$ : Abstand lokaler Erdoberflächenpunkte zur senkrechten Erdachse $R_{pole}$
$R_{\varphi}$ : Radius Erde Oberfläche - Mittelpunkt (1)

(1) liefert zwei Erdradien in Abhängigkeit von $\varphi$:
$R_{\varphi_0}$ und $R_{\varphi_1}$ und damit
$R_{m}$ : mittlerer Erdradius an Koordinaten $P_0$ und $P_1$

$R_{m} = \dfrac{R_{\varphi_0} + R_{\varphi_1}}{2}$

Lokaler linearer Ansatz:
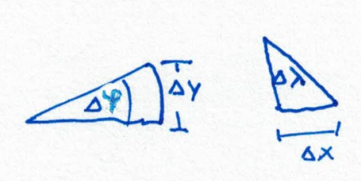
2205211905_GpsDistance01.png $\dfrac{\Delta \lambda}{2 \pi} = \dfrac{\Delta x}{2 \pi R_m}$
$\dfrac{\Delta \varphi}{2 \pi} = \dfrac{\Delta y}{2 \pi R_m}$




Daraus ergeben sich $dx$, $dy$ und $ds$ zu:
2205211906_GpsDistance02.png $\boxed{\Delta x = R_m \Delta \lambda}$
$\boxed{\Delta y = R_m \Delta \varphi}$
$\boxed{\Delta s = \sqrt{{\Delta x}^2 + {\Delta y}^2}}$



WebSites    Module    Mathematik