Kapitel 1 : Magnetismus
1.1 Magnete und ihre Wirkungen
1.2 Das magnetische Feld
1.3 Die magnetische Wirkung des Stromes
1.4 Elektromotoren
1.5 Kraft auf stromdurchflossene Leiter
Quellen
Schmöger, Stötzer: "Impulse Physik Klasse 9/10" [ISBN: 978-3-12-772544-5]Klett Verlag : Impulse Physik 9/10
OpenAI : ChatGPT
Microsoft - Bing : Bing - ChatGPT
Fachbereich Physik : Die magnetische Wirkung des elektrischen Stroms
LEIFIphysik : Magnetisches Feld - Spule
Wikipedia : Neodym-Eisen-Bor - Neodymmagnet
Wikipedia : Magnetische Feldstärke
Wikipedia : Magnetische Feldkonstante
Wikipedia : Magnetische Permeabilität
Wikipedia(en) : Morse Code
1.3 Die magnetische Wirkung des Stromes
Sichtbarmachung der Kraftwirkung des elektrischen Stromes
Versuch 1: Magnetische Kraftwirkung eines stromdurchflossenen Leiter auf eine KompassnadelVersuch 1.1: Fliesst durch einen Leiter ein Strom (Glühlampe leuchtet!), so lenkt die Kompassnadel von ihrer Stellung parallel zum Leiter links senkrecht zum Leiter.
Versuch 1.2: Unterbrechen wir den Stromfluss (Glühlampe leuchtet nicht!), so richtet sich die Kompassnadel wieder parallel zum Leiter und damit in Richtung des Erdmagnetfeldes aus.
Versuch 1.3: Kehren wir den Strom um (Glühlampe leuchtet wieder!), so lenkt die Kompassnadel von ihrer Stellung parallel zum Leiter senkrecht zum Leiter rechts (damit in entgegengesetzter Richtung zu 1.1 !).
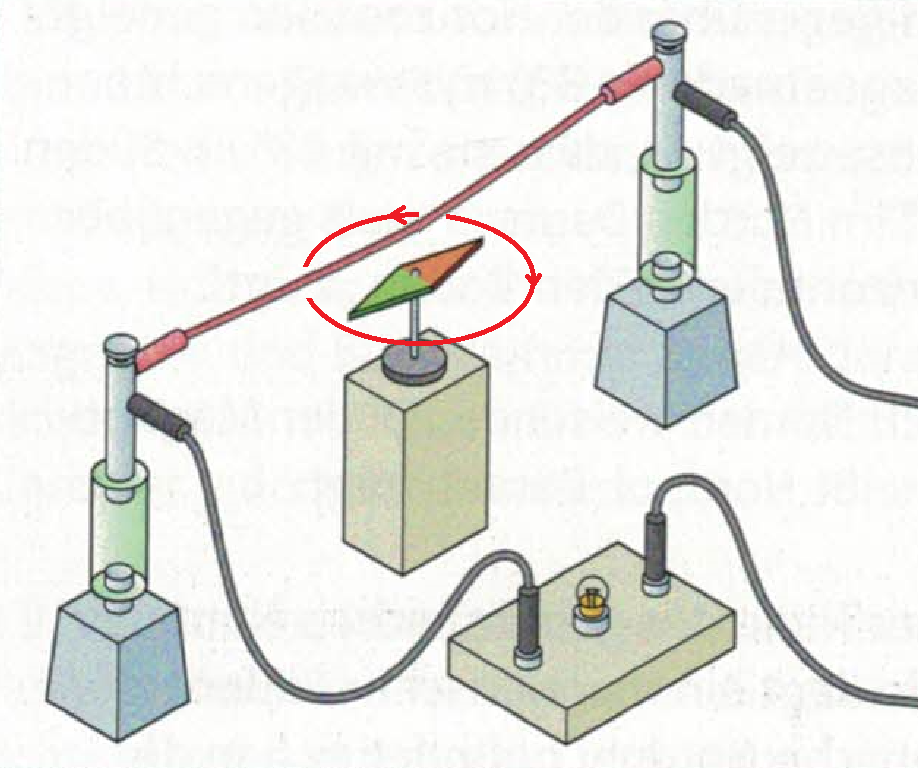
Versuch 2: Geschlossene magnetische Feldlinie um einen stromdurchflossenen Leiter
Versuch 2.1: Der elektrische Leiter wird in Nord-Süd-Richtung ausgerichtet, ohne dass die Spannung eingeschaltet wird.
Versuch 2.2: Man stellt die Kompassnadel unter den elektrischen Leiter und verbindet den Leiter mit der Spannungsquelle.
Versuch 2.3: Man kehrt die Polung der Spannungsquelle um.
Versuch 2.4: Die Kompassnadel wird über den Leiter gehalten und die ursprüngliche Polung eingestellt.
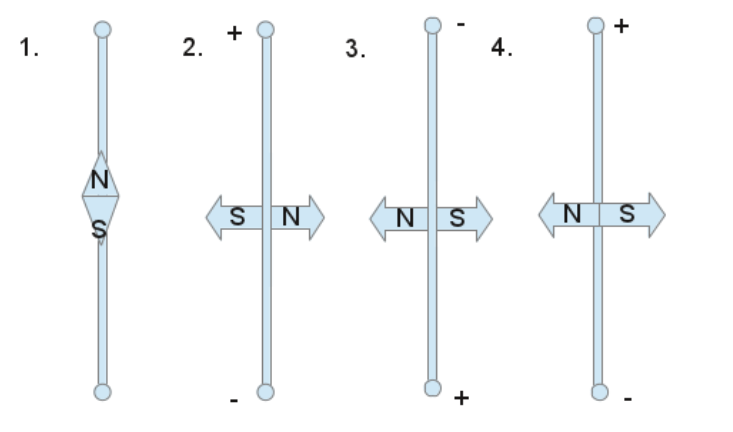
Versuch 2: Beobachtung
zu Versuch 2.1: Die Kompassnadel zeigt zum geographischen Nordpol.
zu Versuch 2.2: Die Kompassnadel stellt sich quer zum Leiter ein und zeigt mit dem Nordpol nach rechts.
zu Versuch 2.3: Die Kompassnadel stellt sich quer zum Leiter ein und zeigt mit dem Nordpol nach links.
zu Versuch 2.4: Die Kompassnadel stellt sich quer zum Leiter ein und zeigt mit dem Nordpol nach links.
Versuch 3: Geschlossene magnetische Feldlinie um einen stromdurchflossenen Leiter
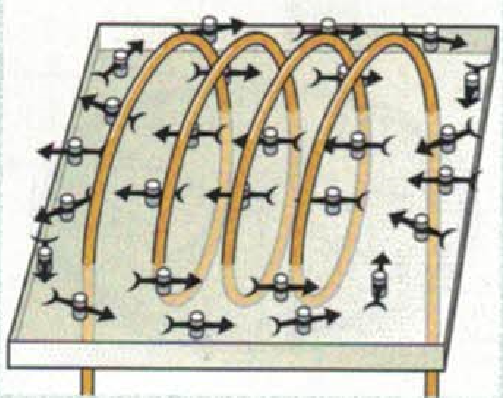
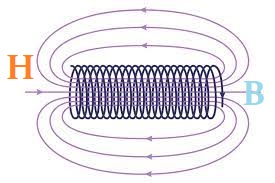
Im Inneren einer (langen) Spule (gegenüber dem Durchmesser) zeigen die Kompassnadeln ein gleichförmiges (homogenes) Magnetfeld.
Im Bild zeigt sich links der Nordpol und rechts der Südpol der Spule
Die magnetischen Feldlinien einer Spule sind von innen nach aussen nach innen geschlossen.
Ändert man die Richtung des Stromes, so wechseln Nord- und Südpol und die Richtungen aller magnetischen Feldlinien.
Definition: Helmholtz-Spule
Eine lange Spule mit einem homogenen Magnetfeld im Innern nennt man auch Helmholtz-Spule.
Elektrischer Strom mit Richtung erzeugt Magnetfeld mit Richtung
Definition: Rechte-Faust-Regel bei geradem Stromleiter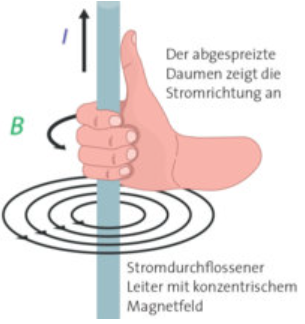

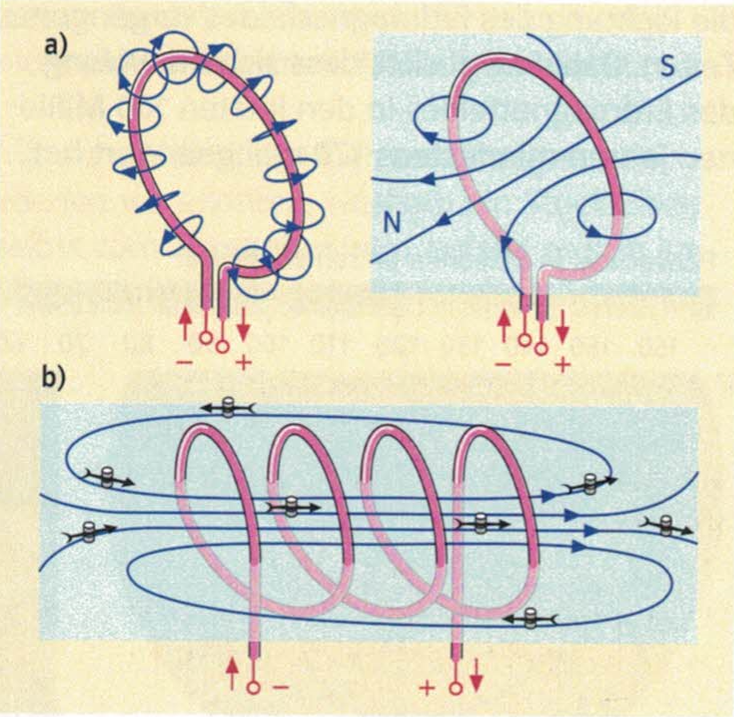
Ergänzung: Genau so gilt die Rechte-Faust-Regel bei einem gebogenen Stromleiter (Beispiel: Kreis):
(a) : Die geschlossenen magnetischen Feldlinien verlaufen auf der Oberfläche eines Schlauches um den Leiter.
(b) : Dabei addieren sich die Richtung und die Stärke der Feldlinien zum Gesamtfeld (Superpositionsprinzip).
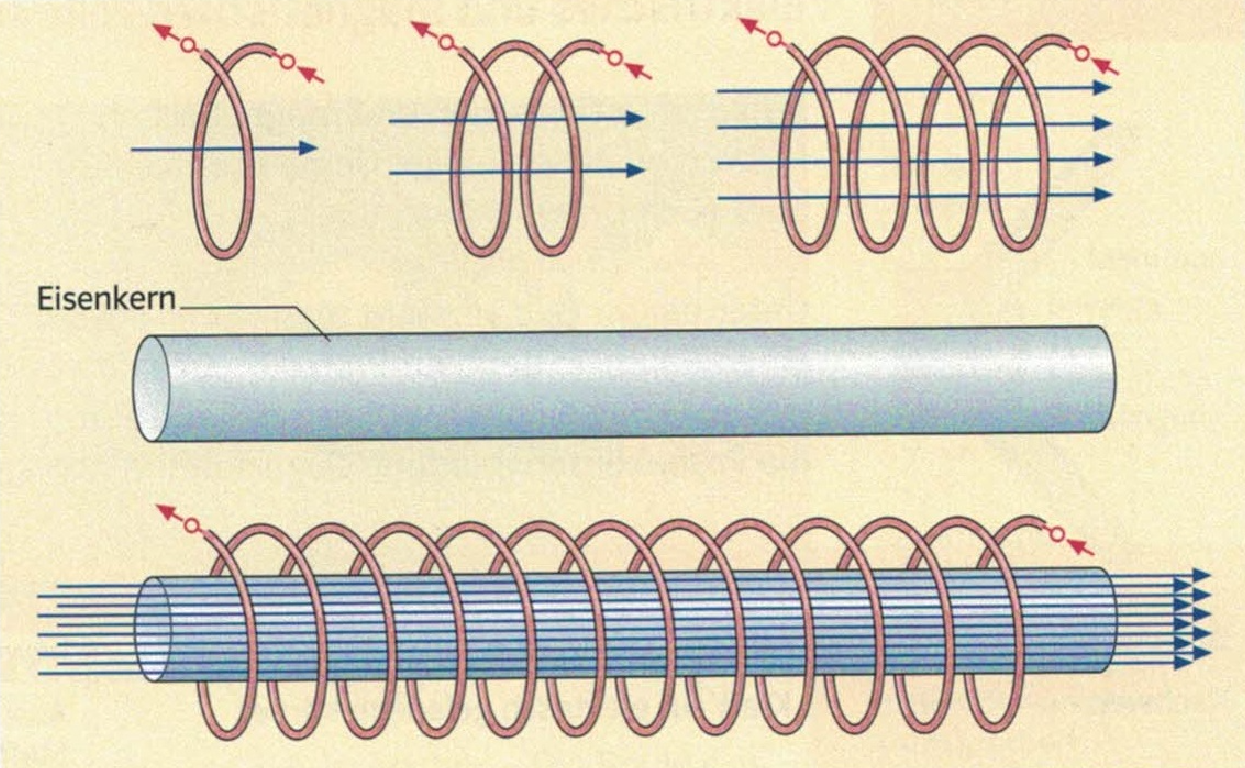
Folgerung: Durch jede weitere Windung der Spule addieren und verstärken sich die Feldlinien zweier parallel zueinander verlaufender Leiter/Windungen (mit gleicher Stromrichtung)!
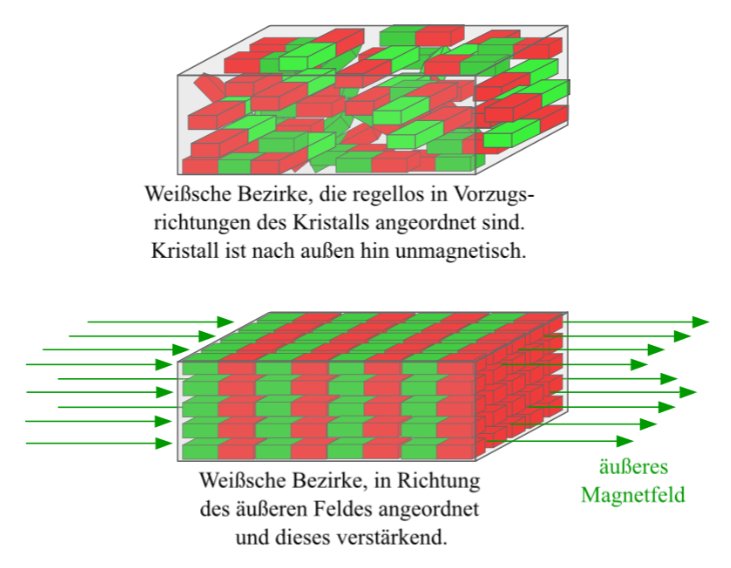
Weisssche Bezirke als Magnetfeld-Verstärker
Folgerung: Eine stromdurchflossene Spule mit einem Eisenstab im Innern wirkt wie ein verstärkter Elektromagnet: das Magnetfeld der Spule wird mit Eisenkern deutlich grösser!
Magnetische Kraft auf Stabmagnet
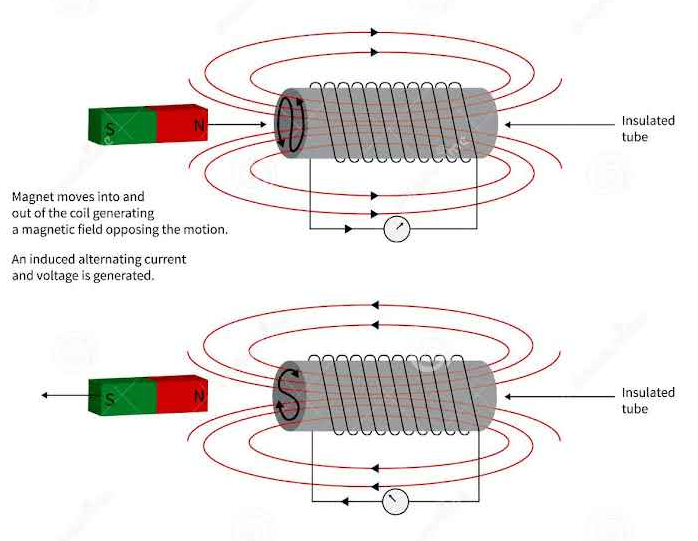
Folgerung: Eine stromdurchflossene Spule wirkt wie ein Elektromagnet:
Ein Stabmagnet wird von der magnetisch aktiven Spule angezogen!
Beobachtung: Eine stromdurchflossene Spule wirkt wie ein Elektromagnet:
Ein ferromagnetischer Körper (oder auch Stabmagnet) wird von der magnetisch aktiven Spule angezogen!
Begründung: Der ferromagnetische Körper wird durch die Fernwirkung des Magnetfelds der Spule magnetisiert und richtet somit die Elementarmagnete in den Weissschen Bezirken aus. Der ferromagnetische Körper wird so zu einem (schwachen) "Stabmagneten" und richtet seinen inversen Pol gegen den Pol des Elektromagneten.
Magnetische Erregung - magnetische Feldstärke
Definition: Die magnetische Erregung $\vec{H}$ ordnet jedem Punkt $P=(x,y,z)$ des Raumes eine Stärke und Richtung des sich ergebenden magnetischen Feldes $\vec{B}$ zu:$\boxed{\vec{B} = \mu \mu_0 \vec{H}}$ (1) : Betrag und Richtung von $H$ und $B$
$\boxed{B = \mu \mu_0 H}$ (1a) : Betrag von $H$ und $B$
$\mu_0$ : Die magnetische Feldkonstante $\mu _{0}$ ist eine physikalische Konstante und gibt die magnetische Permeabilität des Vakuums und damit den Proportionalitätsfaktor zwischen magnetischer Erregung $\vec{H}$ und resultierendem Magnetfeld $\vec{B}$ an. Die magnetische Permeabilität des Vakuums $\mu_0$ beträgt :
$\boxed{\mu_0 = 1.256 \cdot 10^{-6} \dfrac{kg \cdot m}{s^2 \cdot A^2}}$ (2)
$\mu$ : Die magnetische Permeabilität (auch magnetische Leitfähigkeit) bestimmt die Fähigkeit von Materialien, sich einem Magnetfeld anzupassen oder präziser: die Magnetisierung eines Materials in einem äußeren Magnetfeld. Es bestimmt daher die Durchlässigkeit (lateinisch permeare „durchgehen, durchdringen“) von Materie für magnetische Felder:
"Bei gleicher magnetischer Erregung $\vec{H}$ : je grösser die Permeabilität desto grösser das resultierende Magnetfeld $\vec{B}$"
$\boxed{\mu_{eisen} = 300 .. 10000}$ (3)
$\vec{H}$ : Magnetische Erregung, Einheit: $[H] = \dfrac{A}{m}$ (4)
$\vec{B}$ : Magnetisches Feld, magnetische Flussdichte, Einheit: $[B] = \dfrac{N}{A \cdot m} = \dfrac{kg \cdot m}{s^2 \cdot A \cdot m} = \dfrac{kg}{s^2 \cdot A}$ (5)
Betrachtung der Einheiten
$B = \mu \mu_0 H$ (*1a)
$[B] = [\mu] \cdot [\mu_0] \cdot [H]$
$\dfrac{kg}{s^2 \cdot A} = 1 \cdot \dfrac{kg \cdot m}{s^2 \cdot A^2} \cdot \dfrac{A}{m}$
$\dfrac{kg}{s^2 \cdot A } = \dfrac{kg}{s^2 \cdot A^2} \cdot A$
$\dfrac{kg}{s^2 \cdot A } = \dfrac{kg}{s^2 \cdot A}$ (q.e.d)
Die Einheit des magnetischen Feldes $[B] = \dfrac{kg}{s^2 \cdot A}$ ist identisch mit dem
Produkt der Einheiten $[\mu] \cdot [\mu_0] \cdot [H]$ entsprechend dem
Produkt der Einheit(magnetische Permeabilität $\mu$) mal Einheit(magnetische Feldkonstante $\mu_0$) mal Einheit(magnetische Erregung $H$)
Gleichung zur Berechnung der Kraft durch die magnetische Erregung $H$ einer Spule
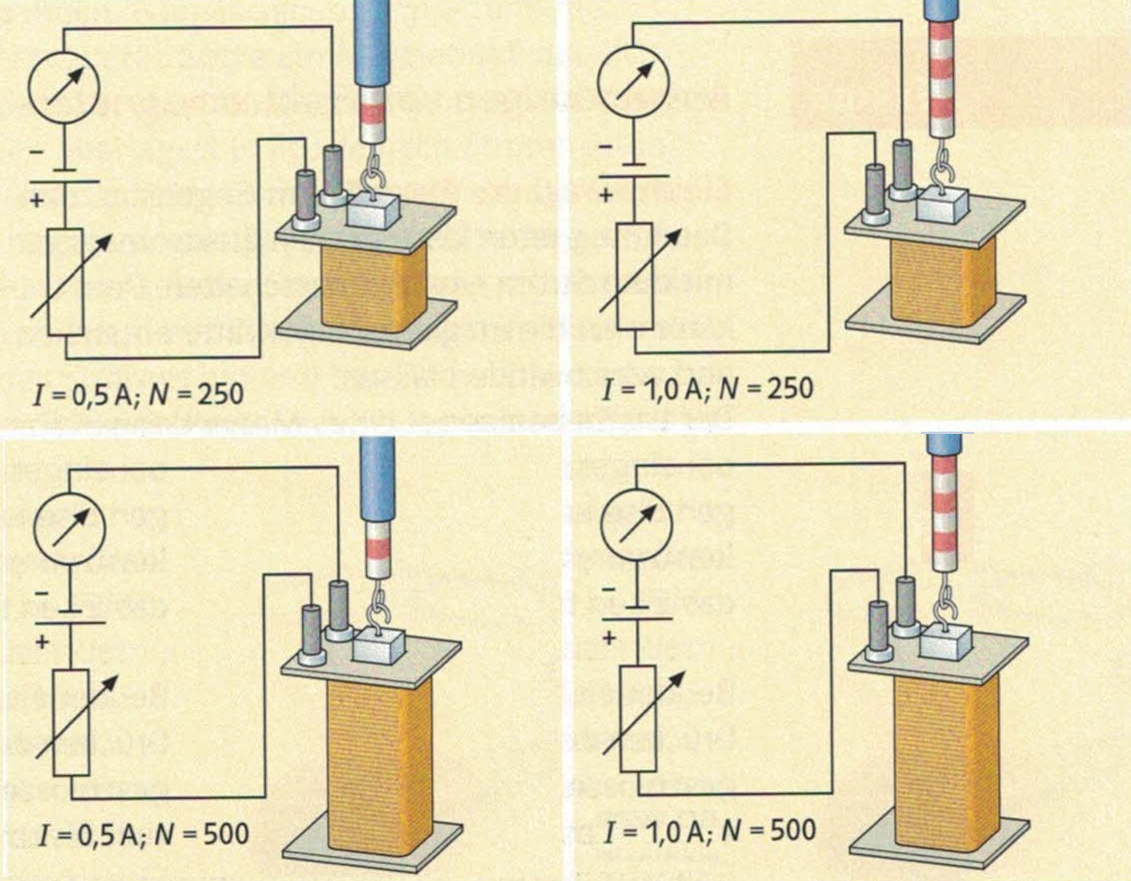
Kraft $F$ einer Spule proportional $\propto$ der Länge $L$, der Windungszahl $N$ und dem Erregerstrom $I$:
$\boxed{F \propto I \cdot \dfrac{N}{L}}$ (6) : magnetische Kraft auf Probekörper im Innern einer Spule
• Kraft $F$ proportional dem Strom $I$
• Kraft $F$ proportional der Windungszahl $N$
• Kraft $F$ umgekehrt proportional der Länge $L$
Magnetische Erregung $H$ im Innern einer langen Spule
$\boxed{H = I \cdot \dfrac{N}{L}}$ (7)
Magnetisches Feld $B$ im Innern einer langen Spule
$B = \mu \mu_0 H$ (*1a) $\Rightarrow H = \dfrac{B}{\mu \mu_0}$ $\Rightarrow \dfrac{B}{\mu \mu_0} = I \cdot \dfrac{N}{L}$
$\boxed{B = \mu \mu_0 \cdot I \cdot \dfrac{N}{L}}$ (8)
Ergebnis:
Damit hängt im Innern einer langen Spule die Kraft $F$:
$\boxed{F \propto H}$ und damit auch $\boxed{F \propto B}$ (9)
proportional vom der magnetischen Erregung $H$ und der magnetischen Feldstärke $B$ ab.
Versuch zur Stärke des Magnetfelds einer Spule
Neodym-Magnet
Neodym-Magnete bestehen aus Neodym-Eisen-Bor. Mit der 1986 gefundenen Seltene-Erden-Legierung Nd2Fe14B werden die zur Zeit stärksten Dauermagnete hergestellt.Neodym-Magnete finden sich in Lautsprechern, Elektromotoren, Schreib-Lese-Köpfen von Festplatten...
Neodym-Magnete tragen ungefähr das 1000-fache ihres Eingengewichts.

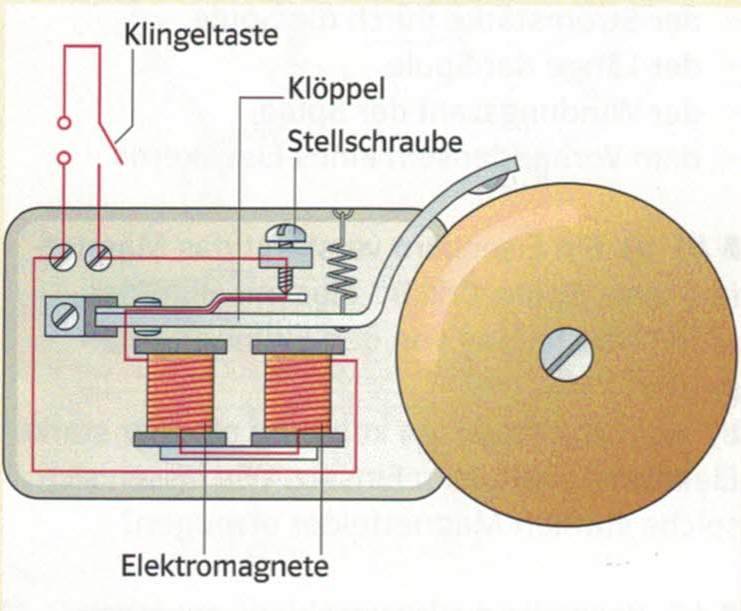
Anwendung Elektromagnet: Elektrische Klingel
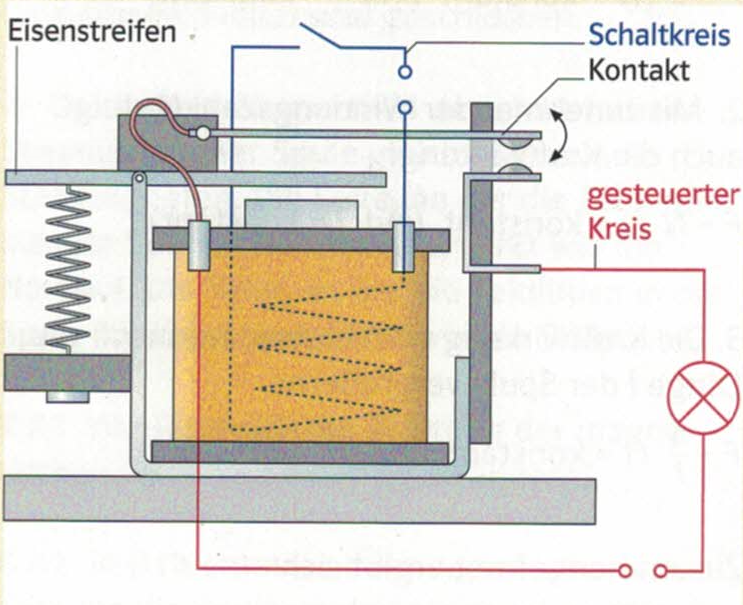
Anwendung Elektromagnet: Relais
Anwendung Elektromagnet: Lautsprecher
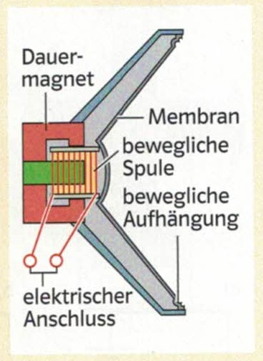
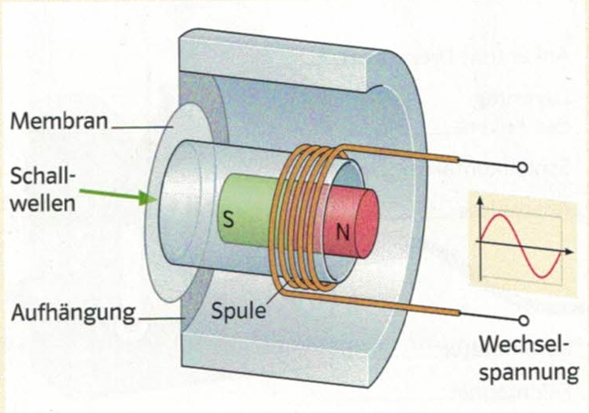

Anwendung Elektromagnet: Mikrofon

Anwendung Elektromagnet: Festplatte

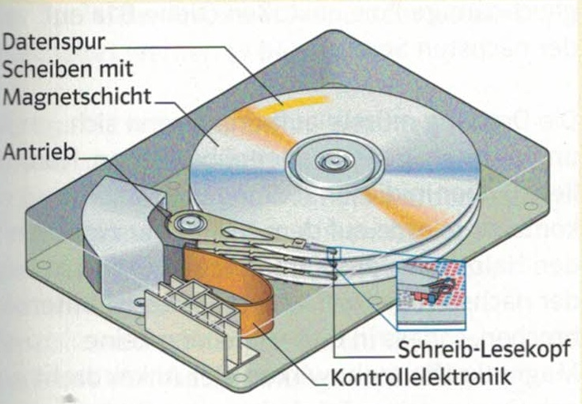
Anwendung Elektromagnet: Morse-Sender und -Empfänger

Elektrisches und Magnetisches Feld im Vergleich

Homepage WebSites Unterrichtsstunden Mathematik