Algebra - Funktionen
Übersicht
Unterscheidung von Funktionsarten:• Konstante Funktionen
• Lineare Funktionen
• Quadratische Funktionen
• Kubische Funktionen
• Polyomfunktionen
Konstante Funktionen
$\boxed{f(x) = y = C}$ mit $C, y \in \mathbb{R}$Definition Konstante Funktion: $f(x) = y(x) = y = C$
Achsenabschnitt: $\boxed{C}$
Nullstelle: keine Nullstelle für $C \neq 0$, ausser $C = 0$ (Funktion identisch der x-Achse)
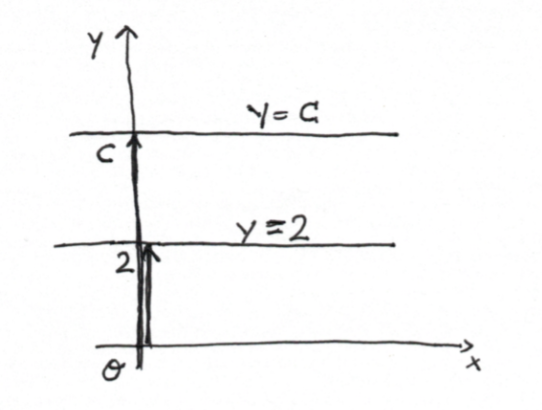
Beispiel: $f(x) = y = 2$
mit Funktionsverlauf: Konstante Gerade parallel mit Abschnitt $C$ parallel zur y-Achse
Lineare Funktionen
$\boxed{f(x) = y = m x + b}$ mit $m, b, x, y \in \mathbb{R}$Definition Lineare Funktion: $f(x) = y(x) = y = m \cdot x + b = m x +b$
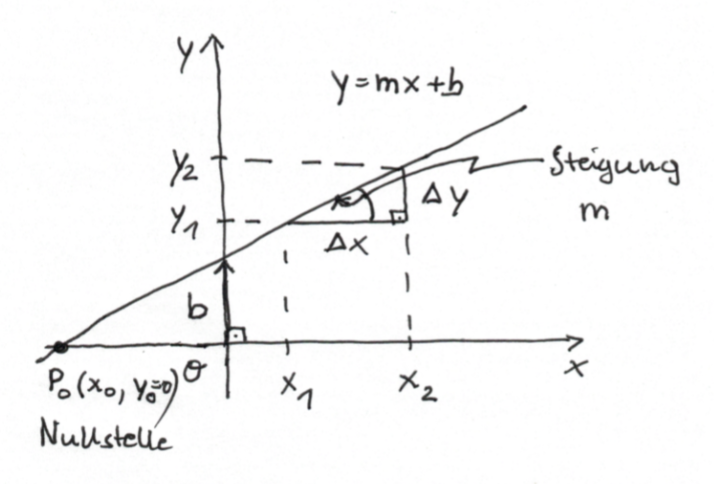
Achsenabschnitt: $\boxed{b = y(x = 0)}$
Steigung: $\boxed{m = \dfrac{y_2 - y_1}{x_2 - x_1}}$
Nullstelle: $y_0 = 0 = m x_0 + b$ $\Rightarrow -b = m x_0$ $\boxed{x_0 = -\dfrac{b}{m}}$
Beispiel: $f(x) = y = 2 x + 1$
mit Funktionsverlauf: Gerade mit positiver Steigung $m = 2$ und Achsenabschnitt $b = 1$
Quadratische Funktionen
$\boxed{f(x) = y = a x^2 + b x + c}$ mit $a, b, c, x, y \in \mathbb{R}$Definition Quadratische Funktion: $f(x) = y(x) = y = a x^2 + b x + c$
Nullstellen: !!! wird noch nachgereicht !!!
Beispiel: $f(x) = y = \dfrac{x^2}{2} + 2 x +1$
mit Funktionsverlauf: nach oben geöffnete Parabel mit Verschiebung in x- und y-Richtung.
Kubische Funktionen
$\boxed{f(x) = y = a x^3 + b x^2 + c x + d}$ mit $a, b, c, d, x, y \in \mathbb{R}$Definition Kubische Funktion: $f(x) = y(x) = y = a x^3 + b x^2 + c x + d$
Nullstellen: !!! wird noch nachgereicht !!!
Beispiel: $f(x) = y = 2 x^3 + x^2 + 2 x + 3$
Polynomfunktionen
$\boxed{f(x) = y = \sum_{i = 0}^{n}{a_i x^i}}$ mit $a_i, x_i, y \in \mathbb{R}$Definition Polynomfunktion: $f(x) = y(x) = y = \sum\limits_{i = 0}^{n}{a_i x^i}$
$ \Leftrightarrow y = a_0 + a_1 x + a_2 x^2 + .. + a_n x^n$
Nullstellen: !!! wird noch nachgereicht !!!
Beispiel: $f(x) = y = 2 x^5 - x^4 + 2 x^3 - 3 x^2 + 2 x - 1$
WebSites Module Mathematik