Differentialgeometrie - Bogenlänge

Übersicht

Berechnet wird die Bogenlänge $s$ einer Parameterform $\vec{P}(t)$ im $\mathbb{R^N}$ mit:

$s = +\sqrt{\bigg[\dfrac{dx(t)_1}{dt}\bigg]^2 + \bigg[\dfrac{dx(t)_2}{dt}\bigg]^2 + .. \bigg[\dfrac{dx(t)_N}{dt}\bigg]^2} dt = +\sqrt{\sum\limits_i^N \bigg[\dfrac{dx_i}{dt}\bigg]^2} dt$

Dabei ist $N \in \mathbb{N_1}$ die Dimensionszahl mit $N \geq 1$ ,
$x(t)_i, i \in [1,2, .. ,N]$ die für jede Dimension anteiliegen Parameterfunktionen der Parameterform $\vec{P}(t)$ und
$t \in \mathbb{R}$ der (einzige) freie Parameter der Parameterform $\vec{P}(t)$ .
Im Spezialfall der normierten Parameterform $\vec{P}(t)$ beschränkt sich $t$ auf den Bereich $t \in [0 .. 1]$

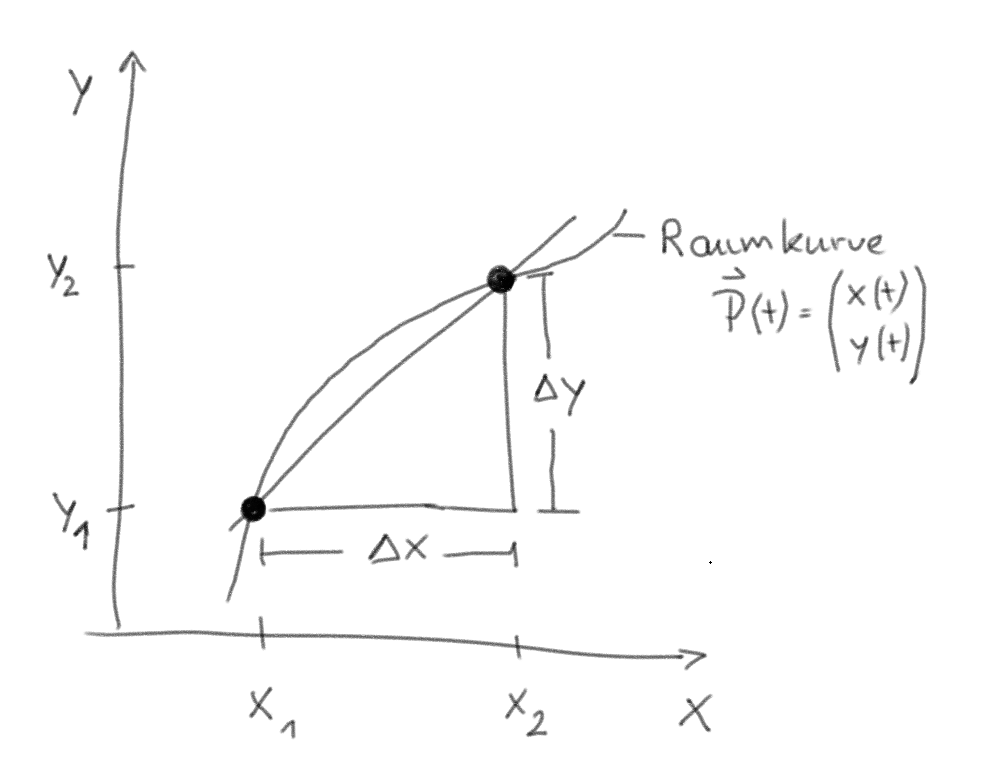
Herleitung

Parameterform $\vec{P}(t)$ mit Parameter $t \in \mathbb{R}$ in $N \in \mathbb{N_1}$ Dimensionen:

$\vec{P}(t) = \begin{pmatrix} P_1(t) \\ P_2(t) \\ .. \\ P_N(t) \\ \end{pmatrix}$

$P_1(t), P_2(t), ...$ entsprechen den reellwertigen Funktionen $P_x(t), P_y(t), ...$

und besitzen als Bild eine Raumkurve in $\mathbb{R^N}$ .
Beschreiben wir nun die Raumkurve einer gegebenen Parameterform
näherungsweise mit einem diskreten Polygonzug (lineare Kurvenapproximation),
so beträgt die Länge $s$ des Polynomzuges (mit Pythagoras im $\mathbb{R^N}$) :

$\Delta s^2 = \sum\limits_i^N \Delta x_i^2$    $\bigg| \dfrac{1}{\Delta t^2}$

$ \lim\limits_{\Delta t \to 0}$    $\bigg[\dfrac{\Delta s}{\Delta t}\bigg]^2 = \sum\limits_i^N \bigg[\dfrac{\Delta x_i}{\Delta t}\bigg]^2$

$\bigg[\dfrac{ds}{dt}\bigg]^2 = \sum\limits_i^N \bigg[\dfrac{dx_i}{dt}\bigg]^2$

$\dfrac{ds}{dt} = +\sqrt{\sum\limits_i^N \bigg[\dfrac{dx_i}{dt}\bigg]^2}$

und damit :
$\boxed{ds = +\sqrt{\sum\limits_i^N \bigg[\dfrac{dx_i}{dt}\bigg]^2} dt}$

---

WebSites    Module    Mathematik