Geometrie - Kreis durch 3 Punkte
Quellen
Matheseiten von Arndt Brünner : Kreis durch drei PunkteGegeben & Gesucht
Folgendes Problem wird durch zwei Dimensionen in der $X/Y$-Ebene beschrieben: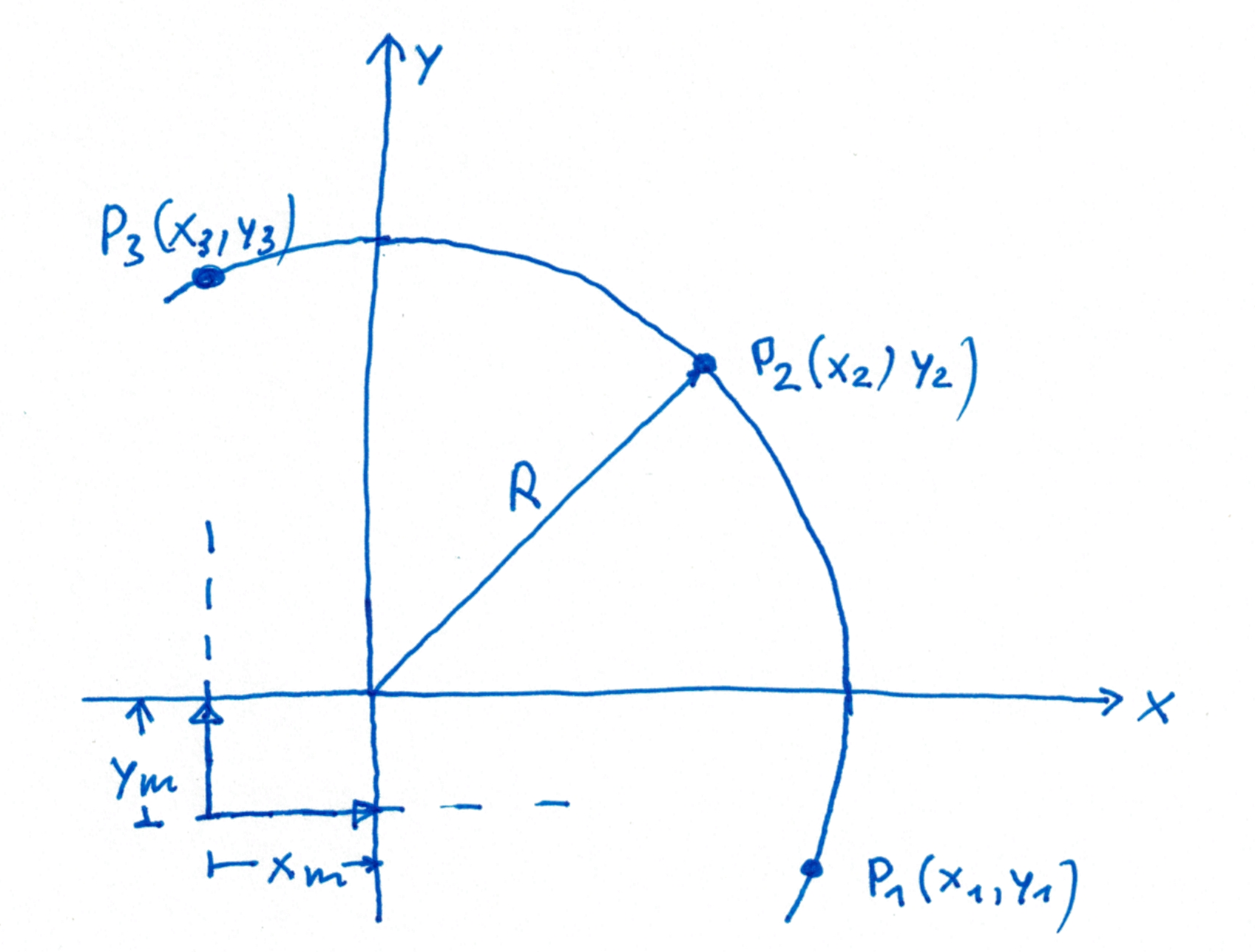
Gesucht wird der Kreis, welcher bei gegebenen drei Punkten
Gegeben: $\boxed{P_1(x_1,y_1)}$ (1.1), $\boxed{P_2(x_2,y_2)}$ (1.2) und $\boxed{P_3(x_3,y_3)}$ (1.3)
durch eben diese Punkte exakt verläuft.
Dabei liegen alle drei Punkte an unterschiedlichen Positionen. Damit sind alle
drei Punkte sind in beiden und nicht nur in einer Koordinate unterschiedlich!
Weiterhin kann der gesuchte Kreis einen Mittelpunkt deckungsungleich zum
Koordinatenursprung besitzen:
Kreisgleichung Mittelpunktsverschiebung: $\boxed{(x - x_m)^2 + (y - y_m)^2 = R^2}$ (2)
Daher werden die Grössen $\boxed{x_m = ?}$ (3.1), $\boxed{y_m = ?}$ (3.2) und $\boxed{R = ?}$ (3.3) gesucht!
Lösung
mit den drei bekannten Punkten $P_1(x_1,y_1)$, $P_2(x_2,y_2)$ und $P_3(x_3,y_3)$ berechnen sichsich die gesuchten Grössen $x_m$, $y_m$ und $R$ über die Zwischengrössen $T$, $T_1$, $T_2$ und $T_3$
und $A$, $B$ und $C$ folgendermassen:
$\boxed{T = (x_2 y_3 - x_3 y_2) - (x_1 y_3 - x_3 y_1) + (x_1 y_2 - x_2 y_1)}$ (vgl. 13* Herleitung)
$\boxed{T_1 = k_1(x_2 y_3 - x_3 y_2) - k_2(x_1 y_3 - x_3 y_1) + k_3(x_1 y_2 - x_2 y_1)}$
$\boxed{T_2 = (k_2 y_3 - k_3 y_2) - (k_1 y_3 - k_3 y_1) + (k_1 y_2 - k_2 y_1)}$
$\boxed{T_3 = (k_3 x_2 - k_2 x_3) - (k_3 x_1 - k_1 x_3) + (k_2 x_1 - k_1 x_2)}$
$\boxed{A = \dfrac{T_1}{T}}$ $\boxed{B = \dfrac{T_2}{T}}$ $\boxed{C = \dfrac{T_3}{T}}$ (vgl. 11* Herleitung)
$\boxed{x_m = -\dfrac{B}{2}}$ $\boxed{y_m = -\dfrac{C}{2}}$ $\boxed{R^2 = x_m^2 + y_m^2 - A}$ (vgl. 14* Herleitung)
Herleitung
Da alle drei Punkte $P_1$, $P_2$ und $P_3$ auf einem Kreis liegen, müssen alle drei Punkteauch Gleichung (2) erfüllen. Einsetzung ergibt:
$(x_1 - x_m)^2 + (y_1 - y_m)^2 = R^2$ (4*)
$(x_2 - x_m)^2 + (y_2 - y_m)^2 = R^2$
$(x_3 - x_m)^2 + (y_3 - y_m)^2 = R^2$
Ausmultiplizieren aller Klammern:
$(x_1 - x_m) \cdot (x_1 - x_m) + (y_1 - y_m) \cdot (y_1 - y_m) = R^2$
$\Rightarrow$ $x_1^2 + x_m^2 -2 x_1 x_m + y_1^2 + y_m^2 - 2 y_1 y_m = R^2$ (5*)
$x_2^2 + x_m^2 -2 x_2 x_m + y_2^2 + y_m^2 - 2 y_2 y_m = R^2$
$x_3^2 + x_m^2 -2 x_3 x_m + y_3^2 + y_m^2 - 2 y_3 y_m = R^2$
Zusammenfassung der unbekannten und gesuchten Grössen:
$\boxed{A := x_m^2 + y_m^2 - R^2}$ (6*)
$\boxed{B := -2 x_m}$
$\boxed{C := -2 y_m}$
Für die Gleichungen (5*) mit $i = [1, 2, 3]$ ergibt sich:
$x_i^2 + x_m^2 -2 x_i x_m + y_i^2 + y_m^2 - 2 y_i y_m - R^2$ = 0
$A + x_i^2 - 2 x_i x_m + y_i^2 - 2 y_i y_m = 0$
$A + x_i^2 + B x_i + y_i^2 + C y_i = 0$
$A + B x_i + C y_i = - x_i^2 - y_i^2$
Damit ergibt sich ein lineares Gleichungssystem mit drei Gleichungen
und drei Unbekannten $A$, $B$ und $C$:
$A + x_1 B + y_1 C = -x_1^2 - y_1^2$ (7*)
$A + x_2 B + y_2 C = -x_2^2 - y_2^2$
$A + x_3 B + y_3 C = -x_3^2 - y_3^2$
und mit den Definitionen $\boxed{k_i := -x_i^2 - y_i^2}$ (8*):
$A + x_1 B + y_1 C = k_1$ (9*)
$A + x_2 B + y_2 C = k_2$
$A + x_3 B + y_3 C = k_3$
Entsprechend der Cramerschen Regel ergibt sich die erweiterte Koeffizientenmatrix $M_c$:
$M_c := \begin{pmatrix} 1 & x_1 & y_1 & k_1 \\ 1 & x_2 & y_2 & k_2 \\ 1 & x_3 & y_3 & k_3 \end{pmatrix}$ (10)
und damit folgende Lösungen für $A$, $B$ und $C$:
$A = \dfrac{det\begin{pmatrix} k_1 & x_1 & y_1 \\ k_2 & x_2 & y_2 \\ k_3 & x_3 & y_3 \end{pmatrix}}{det\begin{pmatrix} 1 & x_1 & y_1 \\ 1 & x_2 & y_2 \\ 1 & x_3 & y_3 \end{pmatrix}}$ $B = \dfrac{det\begin{pmatrix} 1 & k_1 & y_1 \\ 1 & k_2 & y_2 \\ 1 & k_3 & y_3 \end{pmatrix}}{det\begin{pmatrix} 1 & x_1 & y_1 \\ 1 & x_2 & y_2 \\ 1 & x_3 & y_3 \end{pmatrix}}$ $C = \dfrac{det\begin{pmatrix} 1 & x_1 & k_1 \\ 1 & x_2 & k_2 \\ 1 & x_3 & k_3 \end{pmatrix}}{det\begin{pmatrix} 1 & x_1 & y_1 \\ 1 & x_2 & y_2 \\ 1 & x_3 & y_3 \end{pmatrix}}$ (12*)
$\boxed{A = \dfrac{T_1}{T}}$ $\boxed{B = \dfrac{T_2}{T}}$ $\boxed{C = \dfrac{T_3}{T}}$ (11*)
entsprechend der Zwischenergebnisse:
$\boxed{T = (x_2 y_3 - x_3 y_2) - (x_1 y_3 - x_3 y_1) + (x_1 y_2 - x_2 y_1)}$ (13*)
$\boxed{T_1 = k_1(x_2 y_3 - x_3 y_2) - k_2(x_1 y_3 - x_3 y_1) + k_3(x_1 y_2 - x_2 y_1)}$
$\boxed{T_2 = (k_2 y_3 - k_3 y_2) - (k_1 y_3 - k_3 y_1) + (k_1 y_2 - k_2 y_1)}$
$\boxed{T_3 = (k_3 x_2 - k_2 x_3) - (k_3 x_1 - k_1 x_3) + (k_2 x_1 - k_1 x_2)}$
Gleichungen (8*), (11*) und (13*) ergeben damit die gesuchten Variablen $A$, $B$ und $C$
Letztendlich berechnen sich damit $x_m$, $y_m$ und $R$ (entsprechend (6*)) zu:
$\boxed{x_m = -\dfrac{B}{2}}$ $\boxed{y_m = -\dfrac{C}{2}}$ $\boxed{R^2 = x_m^2 + y_m^2 - A}$ (14*)
WebSites Module Mathematik