Operational Amplifier - Addition mit Offset

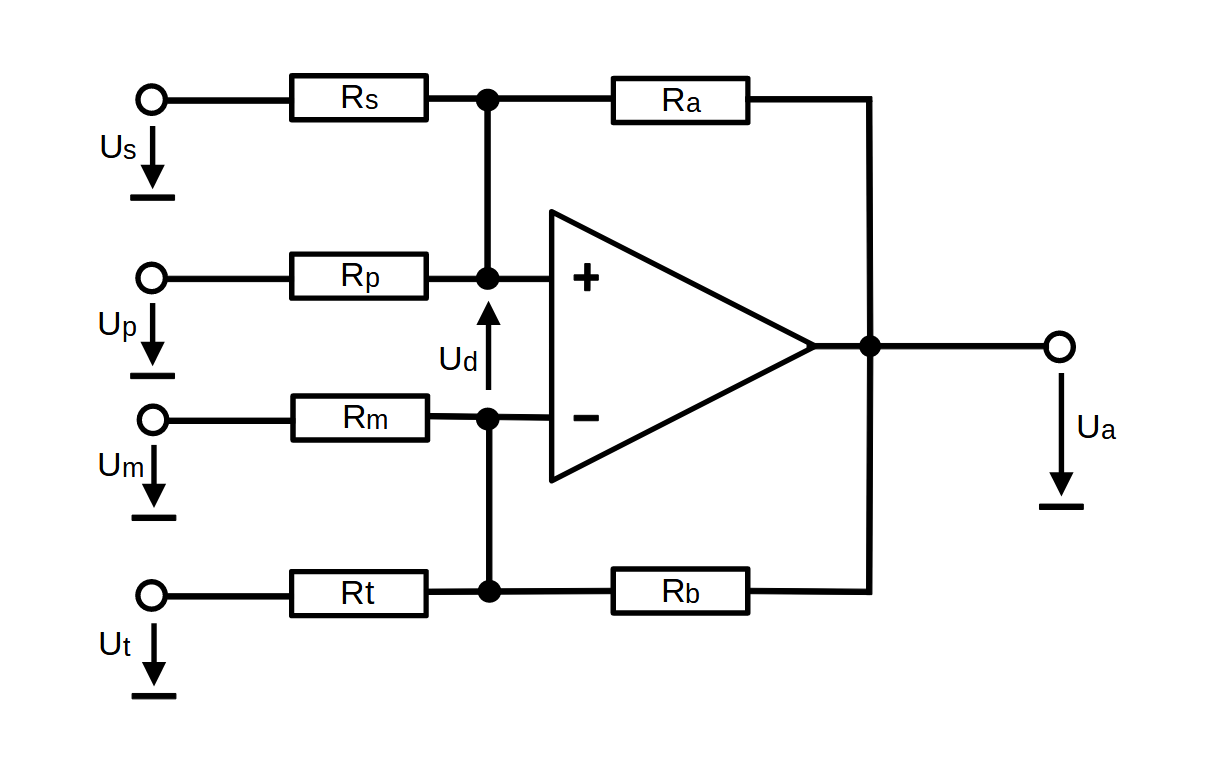
Übersicht

Bekannt: $U_p, U_m, U_s, U_t, R_p, R_m, R_s, R_t, R_a, R_b$

Bedingung: $U_{d} = 0$

Gesucht: Ausgangsspannung $U_a$

Die Ausgangsspannung $U_a$ ergibt sich zu:

$\boxed{U_a = \dfrac{(R_b R_t + R_m R_t + R_b R_m)(R_a R_s U_p + R_a R_p U_s - (R_a R_s + R_a R_p + R_p R_s)(R_b R_t U_m + R_b R_m U_t)}{(R_a R_s + R_a R_p + R_p R_s)R_m R_t - (R_b R_t + R_m R_t + R_b R_m)R_p R_s}}$

Herleitung

Die Ausgangsspannung $U_a$ fällt über dem positiven Zweig des Widerstandsnetzwerkes
$R_a, R_p, R_s$ und dem negativen Zweig des Widerstandsnetzwerkes $R_b, R_m, R_t$ ab.

$U_d = U_+ - U_- = 0 \Rightarrow U_i := U_+ = U_-$ (0)

$\dfrac{U_a - U_i}{R_a} = \dfrac{U_i - U_p}{R_p} + \dfrac{U_i - U_s}{R_s}$ (1)

$\dfrac{U_a - U_i}{R_b} = \dfrac{U_i - U_m}{R_m} + \dfrac{U_i - U_t}{R_t}$ (2)

Elemination von $U_i$:

(1) : $R_p R_s U_a - R_p R_s U_i = R_a R_s U_i - R_a R_s U_p + R_a R_p U_i - R_a R_p U_s$

$R_a R_s U_i + R_a R_p U_i + R_p R_s U_i = R_a R_s U_p + R_a R_p U_s + R_p R_s U_a$

$U_i(R_a R_s + R_a R_p + R_p R_s) = R_a R_s U_p + R_a R_p U_s + R_p R_s U_a$

$U_i = \dfrac{R_a R_s U_p + R_a R_p U_s + R_p R_s U_a}{R_a R_s + R_a R_p + R_p R_s}$

(2) : $R_m R_t U_a - R_m R_t U_i = R_b R_t U_i - R_b R_t U_m + R_b R_m U_i - R_b R_m U_t$

$R_b R_t U_i + R_m R_t U_i + R_b R_m U_i = R_b R_t U_m + R_b R_m U_t + R_m R_t U_a$

$U_i(R_b R_t + R_m R_t + R_b R_m) = R_b R_t U_m + R_b R_m U_t + R_m R_t U_a$

$U_i = \dfrac{R_b R_t U_m + R_b R_m U_t + R_m R_t U_a}{R_b R_t + R_m R_t + R_b R_m}$

$\Rightarrow \dfrac{R_a R_s U_p + R_a R_p U_s + R_p R_s U_a}{R_a R_s + R_a R_p + R_p R_s} = \dfrac{R_b R_t U_m + R_b R_m U_t + R_m R_t U_a}{R_b R_t + R_m R_t + R_b R_m}$

$(R_b R_t + R_m R_t + R_b R_m)(R_a R_s U_p + R_a R_p U_s + R_p R_s U_a) = $
$(R_a R_s + R_a R_p + R_p R_s)(R_b R_t U_m + R_b R_m U_t + R_m R_t U_a)$

$(R_b R_t + R_m R_t + R_b R_m)(R_a R_s U_p + R_a R_p U_s) $
$-(R_a R_s + R_a R_p + R_p R_s)(R_b R_t U_m + R_b R_m U_t) = $
$(R_a R_s + R_a R_p + R_p R_s)R_m R_t U_a - (R_b R_t + R_m R_t + R_b R_m)R_p R_s U_a$

$[(R_a R_s + R_a R_p + R_p R_s)R_m R_t - (R_b R_t + R_m R_t + R_b R_m)R_p R_s] U_a =$
$(R_b R_t + R_m R_t + R_b R_m)(R_a R_s U_p + R_a R_p U_s) $
$-(R_a R_s + R_a R_p + R_p R_s)(R_b R_t U_m + R_b R_m U_t)$

$\boxed{U_a = \dfrac{(R_b R_t + R_m R_t + R_b R_m)(R_a R_s U_p + R_a R_p U_s - (R_a R_s + R_a R_p + R_p R_s)(R_b R_t U_m + R_b R_m U_t)}{(R_a R_s + R_a R_p + R_p R_s)R_m R_t - (R_b R_t + R_m R_t + R_b R_m)R_p R_s}}$

---

WebSites    Module    Elektronik