Definitionen: Zahlenmengen

Quellen

Wikipedia: Natürliche Zahlen
Wikipedia: Ganze Zahlen
Wikipedia: Rationale Zahlen
Wikipedia: Irrationale Zahlen
Wikipedia: Reelle Zahlen

---

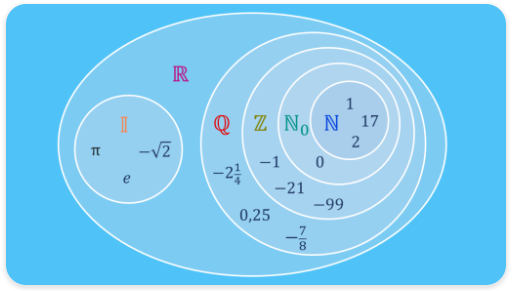
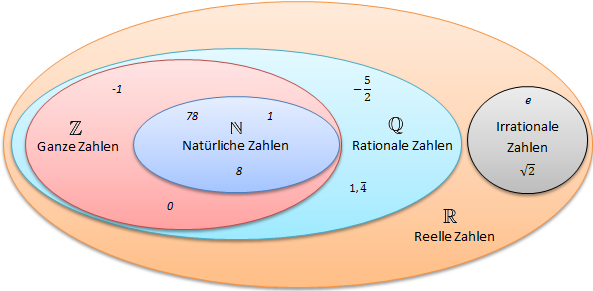
Übersicht Zahlenmengen

  •  Natürliche Zahlen - Symbol: $\mathbb{N}$
  •  Ganze Zahlen - Symbol: $\mathbb{Z}$
  •  Rationale Zahlen - Symbol: $\mathbb{Q}$
  •  Irrationale Zahlen - Symbol: $\mathbb{I}$
  •  Reelle Zahlen - Symbol: $\mathbb{R}$

  •  Die Ganze Zahlen beinhalten die Natürliche Zahlen
  •  Die Rationalen Zahlen beinhalten die Ganzen Zahlen
  •  Die Reellen Zahlen beinhalten die Rationalen Zahlen und die Irrationalen Zahlen

---

Natürliche Zahlen

Die natürlichen Zahlen sind die beim Zählen verwendeten Zahlen (Finger, Steine, ...).
Die Menge aller natürlichen Zahlen kürzen wir ab als: $\boxed{Z_{natuerlich} \in \mathbb{N}}$
und schreiben ausführlich: $\boxed{Z_{natuerlich} \in \{1, 2, 3, 4, 5, 6, .. , 10, 11, .. \}}$

Sonderfall:

Erweiterung der Menge der natürlichen Zahlen mit der Null:
$\boxed{Z_{natuerlich0} \in \{0, 1, 2, 3, 4, 5, 6, .. , 10, 11, .. \}}$

Die Menge der natürlichen Zahlen einschliesslich der Null kürzen wir ab als: $\boxed{Z_{natuerlich0} \in \mathbb{N_0}}$

---

Ganze Zahlen

Die ganzen Zahlen erweitern die natürlichen Zahlen um die negativen ganzen Zahlen und die Null:
$\boxed{Z_{ganz} \in \{-6, -5, -4, -3, -2, -1, 0, +1, +2, +3, +4, +5, +6, .. \}}$

Die Menge aller ganzen Zahlen kürzen wir ab als: $\boxed{Z_{ganz} \in \mathbb{Z}}$

---

Rationale Zahlen

Eine rationale Zahl ist eine Bruchzahl und kann als Verhältnis (lateinisch ratio) zweier ganzer Zahlen dargestellt werden.
Die Menge aller Rationalen Zahlen kürzen wir ab als: $\boxed{Z_{rational} \in \mathbb{Q}}$

Beispiel:

Teilt man ganzen Zahlen $3$ und $2$, so ergibt sich die rationale Zahl $1.5$ :

$\boxed{3 / 2 = \dfrac{3}{2} = 1.5}$ mit $2 \in \mathbb{N}$ , $3 \in \mathbb{N}$ und $1.5 \in \mathbb{Q}$

$\boxed{1 / 7 = \dfrac{1}{7} = 0.142857142857142857142857142857 .. = 0.\overline{142857}}$ mit $1 \in \mathbb{N}$ , $7 \in \mathbb{N}$ und $\dfrac{1}{7} \in \mathbb{Q}$

Sonderfall:

Die ganzen Zahlen sind Bestandteil der rationalen Zahlen
$6 / 3 = \dfrac{6}{3} = 2$ mit $\{2, 3, 6\} \in \mathbb{N}$

---

Irrationale Zahlen

 •  Eine irrationale Zahl ist eine nicht periodische Dezimalzahl mit einer unendlichen Anzahl von Dezimalstellen.
 •  NegativDefinition: eine irrationale Zahl kann nicht als eine Bruchzahl und damit nicht als Verhältnis
     zweier ganzer Zahlen dargestellt werden.
 •  Die Menge aller Rationalen Zahlen kürzen wir ab als: $\boxed{Z_{irrational} \in \mathbb{I}}$

Beispiele:

 •  Darstellung einer irrationalen Zahl als unendliche nichtperiodischer Dezimalzahl:
     $Z_{irrational} = 0.10101110010101011001010000011011 .. 0010110101 .. \in \mathbb{I}$ (nicht periodisch!)
 •  Zahl Pi : $\boxed{\pi = 3.14159265358979323846264338327950288419716939937510 .. \in \mathbb{I}}$
 •  Eulersche Zahl : $\boxed{e = 2.7182818284590452353602874713526624977572 .. \in \mathbb{I}}$

---

Reelle Zahlen

 •  Die Menge aller Reellen Zahlen kürzen wir ab als: $\boxed{Z_{reell} \in \mathbb{R}}$
 •  Damit lassen sich reelle Zahlen entweder als periodische unendliche Dezimalzahl oder als nichtperiodische unendliche Dezimalzahl schreiben.
 •  Wenn eine Zahl entweder eine rationale Zahl oder eine irrationale Zahl ist, ist diese Zahl auch eine reelle Zahl.
 •  Die Menge der reellen Zahlen umfasst die Menge aller rationalen Zahlen und die Menge aller irrationalen Zahlen:
     $\mathbb{R} = \mathbb{Q} \cup \mathbb{I}$ und damit $\mathbb{I} = \mathbb{R} \setminus \mathbb{Q}$ oder $\mathbb{Q} = \mathbb{R} \setminus \mathbb{I}$

Beispiele:

In Anlehnung an die rationalen Zahlen:
Dezimalbruch : $1 / 7 = \dfrac{1}{7} = 0.142857142857 .. = 0.\overline{142857}$ mit $\dfrac{1}{7} \in \mathbb{Q} \in \mathbb{R}$

In Anlehnung an die irrationalen Zahlen:
Zahl Pi : $\pi = 3.14159265358979323846264338327950288419 .. \in \mathbb{I} \in \mathbb{R}$

---

Homepage    WebSites    Unterrichtsstunden    Definitionen