Mathematik - Dimensionen 1D, 2D, 3D

Mathematische Beschreibung der Dimensionen 1D, 2D und 3D bezüglich ihrer geometrischen, algebraischen und analytischen Darstellungen:

1D – Eindimensionale Mathematik

Eine eindimensionale Welt besteht aus einer einzigen Zahlengeraden (z. B. der x-Achse).

1.1. Koordinatensystem

• Jeder Punkt in 1D hat eine Koordinate:
  
  \[P(x), \quad x \in \mathbb{R}\]
• Beispiel: Punkt \(P(3)\) liegt auf der Zahlengeraden bei \(x = 3\).

1.2. Geometrie

• Abstand zwischen zwei Punkten \(A(x_1)\) und \(B(x_2)\):
  
  \[d(A, B) = |x_2 - x_1|\]
• Gerade Linie: Eine Gerade in 1D ist einfach die gesamte Zahlengerade oder eine Teilmenge davon.

1.3. Algebraische Strukturen

• Der Raum ist \(\mathbb{R}\) (die Menge der reellen Zahlen).
• Vektorraum: Vektor in 1D ist eine Zahl \(x\) aus \(\mathbb{R}\).
• Lineare Abbildungen: Eine lineare Transformation ist einfach eine Skalierung \(f(x) = ax + b\).

Quellen:

• Wikipedia - Dimension 1D
  
  

2D – Zweidimensionale Mathematik

Ein zweidimensionaler Raum ist eine Ebene mit zwei unabhängigen Koordinaten.

2.1. Koordinatensysteme

• Kartesisches System:
  Ein Punkt \(P\) hat zwei Koordinaten:
  
  \[P(x, y), \quad x, y \in \mathbb{R}\]
• Polarkoordinaten:
  
  \[x = r \cos \theta, \quad y = r \sin \theta\]

2.2. Geometrie

• Abstand zwischen zwei Punkten \(A(x_1, y_1)\) und \(B(x_2, y_2)\):
  
  \[d(A, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]
• Gerade in 2D:
  
  \[y = mx + b\]
  
  oder allgemeiner
  
  \[ax + by + c = 0\]

2.3. Algebraische Strukturen

• Der Raum ist \(\mathbb{R}^2\) (die Menge aller Paare \((x, y)\)).
• Vektoren in 2D:
  
  \[\vec{v} = \begin{bmatrix} x \\ y \end{bmatrix}\]
• Matrixtransformationen:
  Eine Drehung um \(\theta\) ist eine Multiplikation mit der Rotationsmatrix:
  
  \[R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\]

2.4. Veranschaulichung

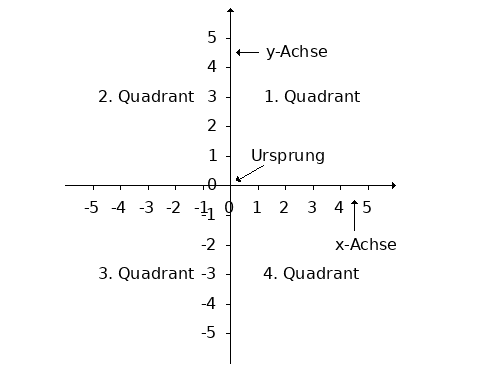
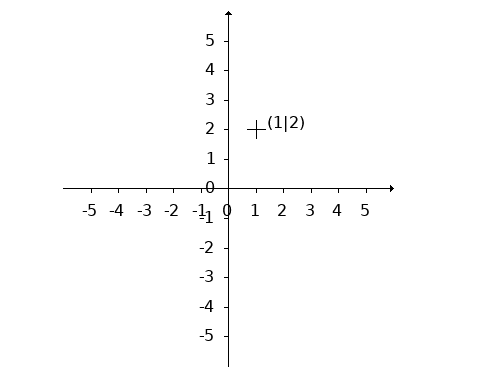
Quellen:

• Wikipedia - Dimension 2D
  
  

3D – Dreidimensionale Mathematik

Ein dreidimensionaler Raum hat drei unabhängige Koordinaten.

3.1. Koordinatensysteme

• Kartesisches System:
  
  \[P(x, y, z), \quad x, y, z \in \mathbb{R}\]
• Zylinderkoordinaten:
  
  \[x = r \cos \theta, \quad y = r \sin \theta, \quad z = z\]
• Kugelkoordinaten:
  
  \[x = r \sin \theta \cos \phi, \quad y = r \sin \theta \sin \phi, \quad z = r \cos \theta\]

3.2. Geometrie

• Abstand zwischen zwei Punkten \(A(x_1, y_1, z_1)\) und \(B(x_2, y_2, z_2)\):
  
  \[d(A, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}\]
• Ebene in 3D:
  
  \[ax + by + cz + d = 0\]

3.3. Algebraische Strukturen

• Der Raum ist \(\mathbb{R}^3\).
• Vektoren in 3D:
  
  \[\vec{v} = \begin{bmatrix} x \\ y \\ z \end{bmatrix}\]
• Matrixtransformationen in 3D:
  • Drehung um die z-Achse:
    
    \[R_z(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

3.4 Veranschaulichung

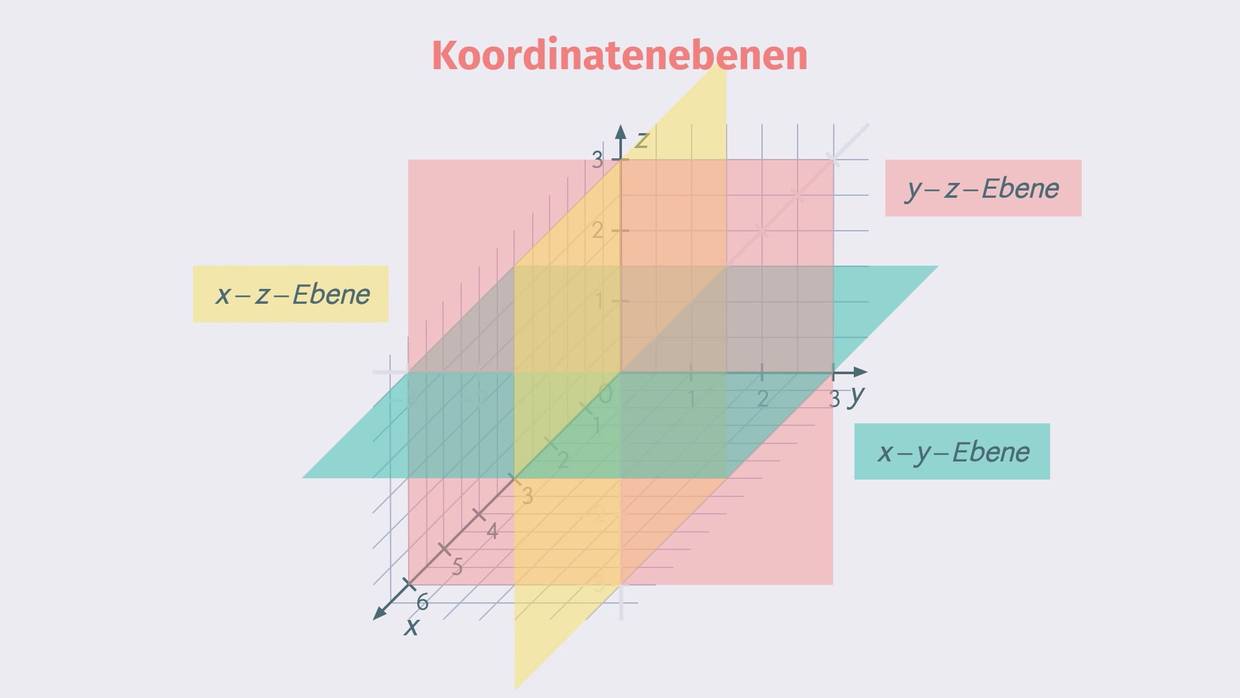
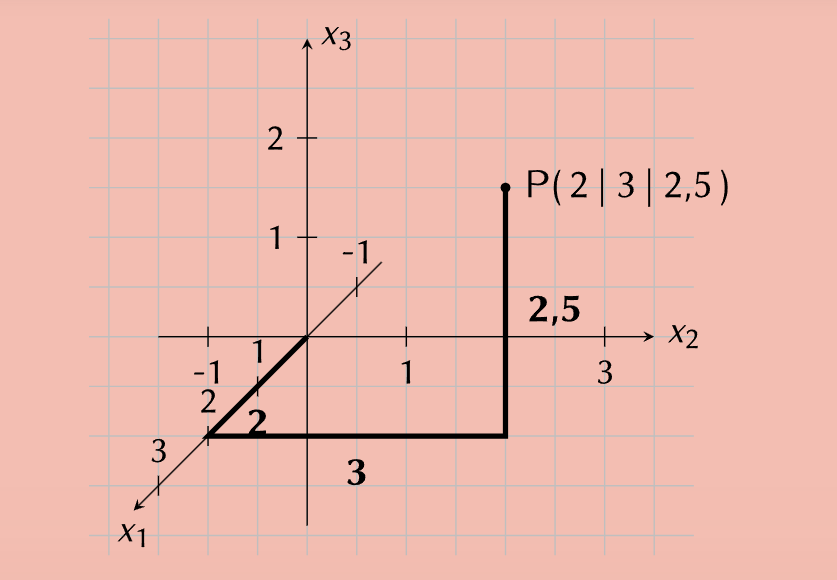
Quellen:

• Wikipedia - Dimension 3D