Mathematik - Relationen und Funktionen
Quellen
- Wikipedia - Bild (Mathematik)
- Wikipedia - Funktionsgraph
- GeoGebra Hauptseite und Calculator / Plotter
- Python/Spyder - Berechne/Plotte Funktionswerte mit Bibliothek MatPlotLib
1. Relationen
Eine Relation ist eine Verknüpfung von Elementen zweier Mengen.
Bild einer Relation (keine Funktion!) der Menge $\mathbb{M}_1$ auf die Menge $\mathbb{M}_2$ :
$\boxed{\mathbb{M}_1 = \{x_1, x_2, x_3\} ~\rightarrow~ \mathbb{M}_2 = \{y_1, y_2, y_3, y_4, y_5\}}$
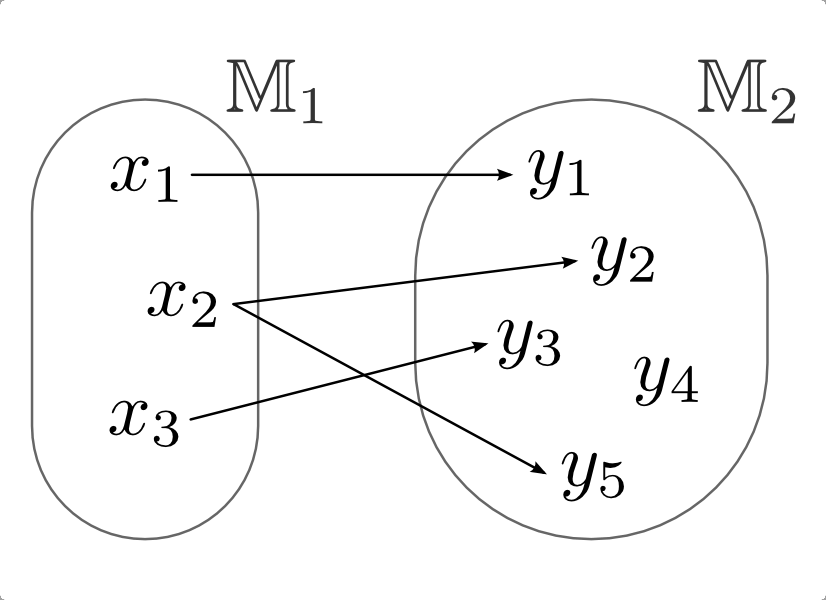
Formal ist eine Relation \(R\) eine Teilmenge des kartesischen Produkts zweier Mengen \(X\) und \(Y\):
\[R \subseteq X \times Y\]
Das bedeutet, dass eine Relation eine Menge von geordneten Paaren \((x, y)\) ist, wobei \(x\) aus der ersten Menge \(X\) und \(y\) aus der zweiten Menge \(Y\) stammt.
Beispiel einer Relation:
Die Relation "größer als" auf den natürlichen Zahlen:
\[R = \{ (2,3), (4,5), (1,6), (3,7) \} \text{ mit } x < y\]
Arten von Relationen:
- Reflexiv: Wenn für alle \(x \in X\) gilt, dass \((x, x) \in R\) (z. B. Gleichheitsrelation).
- Symmetrisch: Wenn aus \((x,y) \in R\) folgt, dass auch \((y,x) \in R\) (z. B. "hat die gleiche Lieblingsfarbe").
- Transitiv: Wenn aus \((x,y) \in R\) und \((y,z) \in R\) folgt, dass auch \((x,z) \in R\) (z. B. "ist größer als").
- Antisymmetrisch: Wenn aus \((x,y) \in R\) und \((y,x) \in R\) folgt, dass \(x = y\) sein muss (z. B. "größer gleich").
2. Funktionen als spezielle Relationen
Eine Funktion ist eine spezielle Relation, bei der jedem Element aus \(X\) genau ein Element aus \(Y\) zugeordnet wird.
Formal: Eine Funktion \(f\) ist eine Relation, die für jedes \(x \in X\) genau ein \(y \in Y\) besitzt, also:
\[\forall x \in X \text{ existiert genau ein } y \in Y \text{ mit } (x,y) \in f\]
Beispiel einer Funktion:
Die Funktion \(f(x) = x^2\) ist eine Relation, die jedem \(x\) genau ein \(y\) zuordnet:
\[(2,4), (-3,9), (0,0) \in f\]
Dies ist eine Funktion, weil kein \(x\) zwei verschiedene \(y\)-Werte hat.
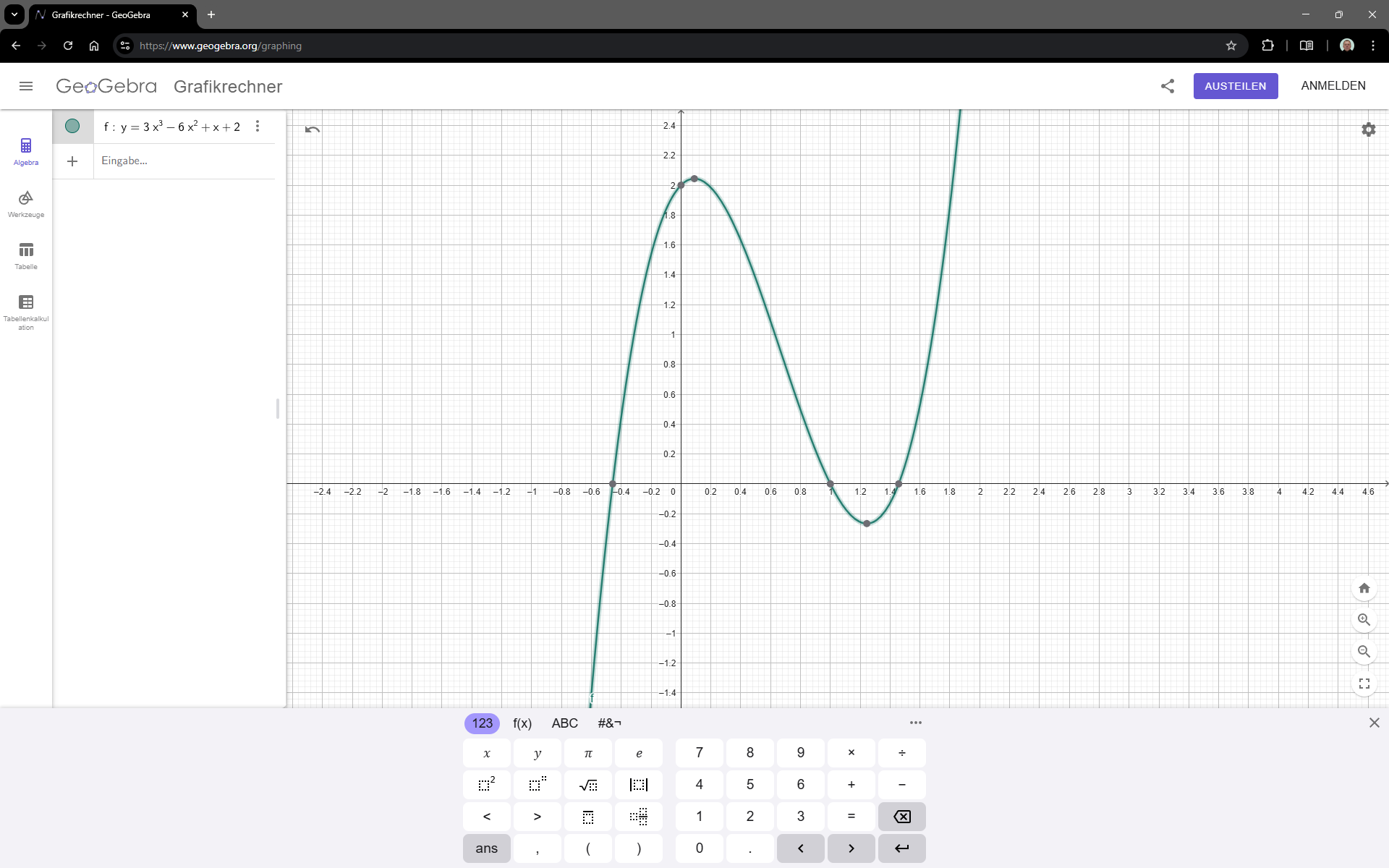
Plot einer Funktion: Polynom 3. Grades
- Gegeben: Polynom-Funktion $y = 3x^3-6x^2+x+2$
- Wertetabelle $~\Rightarrow ~ (x|y)$ Werte in Plot eintragen:
- Graph der Funktion $y = 3x^3-6x^2+x+2$ :
3. Wichtige Unterschiede zwischen Relationen und Funktionen:
| Eigenschaft | Relation | Funktion |
|---|---|---|
| Definition | Menge von geordneten Paaren \((x,y)\) | Spezielle Relation mit eindeutiger Zuordnung |
| Zuordnung $x \Leftrightarrow y$ | - zu einem $x$ kann es mehrere $y$ geben - zu einem $y$ kann es mehrere $x$ geben |
- zu jedem $x$ gibt es nur ein $y$ - zu jedem $y$ kann es mehrere $x$ geben |
| Beispiel | Relation : \((2,3), (2,4)\) | Funktion : \((-2.5, 3), (2, 3), (3,9)\) (Funktion) |