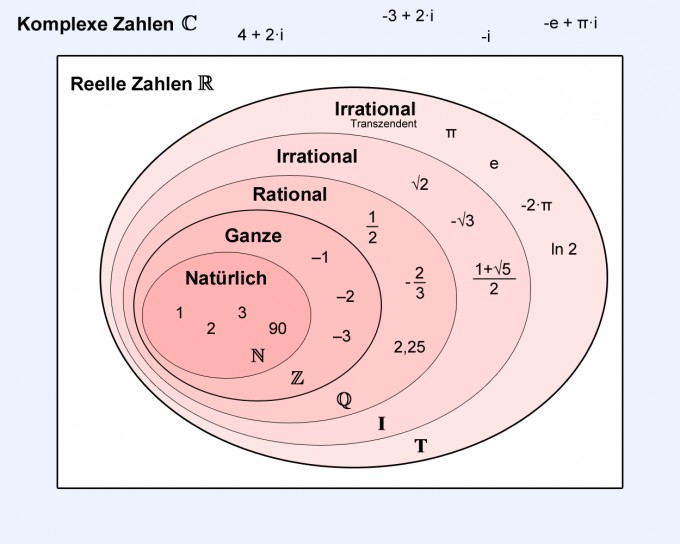
Grundlagen Mathematik - Zahlenmengen
Natürliche Zahlen
| Natürliche Zahlen | $\mathbb{N}$ |
|---|---|
| Umfang | alle positiven ganzen Zahlen |
| Definition | $\mathbb{N} : Z_N \in [1, 2, 3, 4, 5, .. \infty)$ |
| Beispiel | Zahl $1$, $5$ Finger an einer Hand, $10$ Finger an zwei Händen |
Ganze Zahlen
| Ganze Zahlen | $\mathbb{Z}$ |
|---|---|
| Umfang | alle positiven und negativen ganzen Zahlen |
| Definition | $\mathbb{N} : Z_Z \in [1, 2, 3, 4, 5, .. \infty)$ |
| Beispiel | Guthaben: $+5$€ , Schulden: $-5$€ |
Rationale Zahlen
| Rationale Zahlen | $\mathbb{Q}$ |
|---|---|
| Umfang | Verhältnis zweier ganzer Zahlen |
| Definition | $Z_R = \dfrac{p}{q}$ mit $p,q \in \mathbb{Z}$ |
| Beispiel | $Z_R = \dfrac{1}{3} = 0.333..$ |
Irrationale Zahlen
| Irrationale Zahlen | $\mathbb{I}$ |
|---|---|
| Umfang | können nicht als Bruch zweier Ganzer Zahlen dargestellt werden |
| Definition | $Z_R \neq \dfrac{p}{q}$ mit $p,q \in \mathbb{Z}$ |
| Beispiel | $\sqrt{2} = 1.414..$, $\pi = 3.14..$ |
Reelle Zahlen
| Reelle Zahlen | $\mathbb{R}$ |
|---|---|
| Umfang | Gesamtmenge aller Rationalen und Irrationalen Zahlen |
| Definition | $\mathbb{R} : Z_R \in \mathbb{Q} \cup \mathbb{I}$ |
| Beispiel | $1.2345678.., \sqrt{2}, \pi$ |
Komplexe Zahlen
| Komplexe Zahlen | $\mathbb{C}$ |
|---|---|
| Umfang | 2D-Erweiterung der Reellen Zahlen(1D) um eine Imaginäre Dimension(1D) |
| Definition | $i^2 = -1$ allgemein: $Z_R^2 = -Z_{+R} \Rightarrow Z_C = A_R + i \cdot B_R$ |
| Beispiel | $Z_C = \sqrt{-1} = i = 0 + i \cdot 1$ |