KVHS Northeim 2025 : Astronomie - eine Reise durch Raum und Zeit

| Inhalt | Wechselwirkungen im Sonnensystem |

Die Keplerschen Gesetze

Die Keplerschen Gesetze beschreiben die Bewegung der Planeten um die Sonne und wurden vom deutschen Astronomen Johannes Kepler (1571–1630) formuliert. Sie sind grundlegende Gesetze der Himmelsmechanik und bilden die Basis für unser Verständnis des Sonnensystems und der Planetenbewegung. Auch heute sind diese Gesetze entscheidend für Astronomie, Physik und Raumfahrt und gelten nicht nur im Sonnensystem, sondern auch für Exoplaneten und andere kosmische Systeme.

Links

• Wikipedia : Keplersche Gesetze
• LEIFIphysik : Planetensystem - Keplersche Gesetze
• LEIFIphysik : Erstes Keplersches Gesetz
• LEIFIphysik : Zweites Keplersches Gesetz
• LEIFIphysik : Drittes Keplersches Gesetz

Überblick

Die Keplerschen Gesetze als fundamentale Prinzipien der Himmelsmechanik lauten:
1. Keplersches Gesetz:
Planeten bewegen sich auf elliptischen Bahnen mit der Sonne in einem Brennpunkt.
2. Keplersches Gesetz:
Die Geschwindigkeit eines Planeten variiert entlang seiner Bahn, sodass der Fahrstrahl zur Sonne immer gleich große Flächen in gleicher Zeit überstreicht.
3. Keplersches Gesetz:
Die Umlaufzeit eines Planeten hängt mit seiner Entfernung zur Sonne zusammen: $\boxed{T^2 \propto a^3}$

Die Keplerschen Gesetze folgen direkt aus dem Newtonschen Gravitationsgesetz und dessen Anwedung auf die Bedingungen des Zweikörperproblems Sonne-Planet (ebenso: Planet-Mond)

1. Keplersches Gesetz – Das Gesetz der Ellipsen

„Die Planeten bewegen sich auf elliptischen Bahnen, in deren einem Brennpunkt die Sonne steht.“

Erklärung:

• Die Umlaufbahn eines Planeten um die Sonne ist keine perfekte Kreisbahn, sondern eine Ellipse.
• Die Sonne befindet sich nicht im Mittelpunkt der Ellipse, sondern in einem der beiden Brennpunkte.
• Eine Ellipse ist durch zwei Halbachsen gekennzeichnet: die große Halbachse (a) und die kleine Halbachse (b).

Bedeutung:

• Dieses Gesetz widerspricht der früheren Annahme von perfekten Kreisbahnen (nach Ptolemäus und Kopernikus).
• Es erklärt, warum Planeten in bestimmten Bereichen ihrer Bahn weiter von der Sonne entfernt sind und in anderen Bereichen näher.
• Die Exzentrizität einer Ellipse beschreibt, wie „gestreckt“ die Bahn ist. Ist sie nahe 0, ähnelt sie einem Kreis (z. B. fast kreisförmige Bahnen der Erde und Venus).

2. Keplersches Gesetz – Das Flächengesetz

„Ein von der Sonne zum Planeten gezogener Fahrstrahl überstreicht in gleichen Zeiten gleich große Flächen.“

Erklärung:

• Ein Planet bewegt sich schneller, wenn er der Sonne näher ist (Perihel) und langsamer, wenn er weiter entfernt ist (Aphel).
• Das Produkt aus Geschwindigkeit und Abstand zur Sonne bleibt konstant.
• Mathematisch bedeutet das: Die von einem Planeten in einer bestimmten Zeit überstrichene Fläche bleibt immer gleich.

Bedeutung:

• Dieses Gesetz zeigt, dass sich die Planetenbewegung nicht mit konstanter Geschwindigkeit vollzieht, sondern variiert.
• Es ist eine direkte Folge der Gravitationskraft zwischen Sonne und Planet.
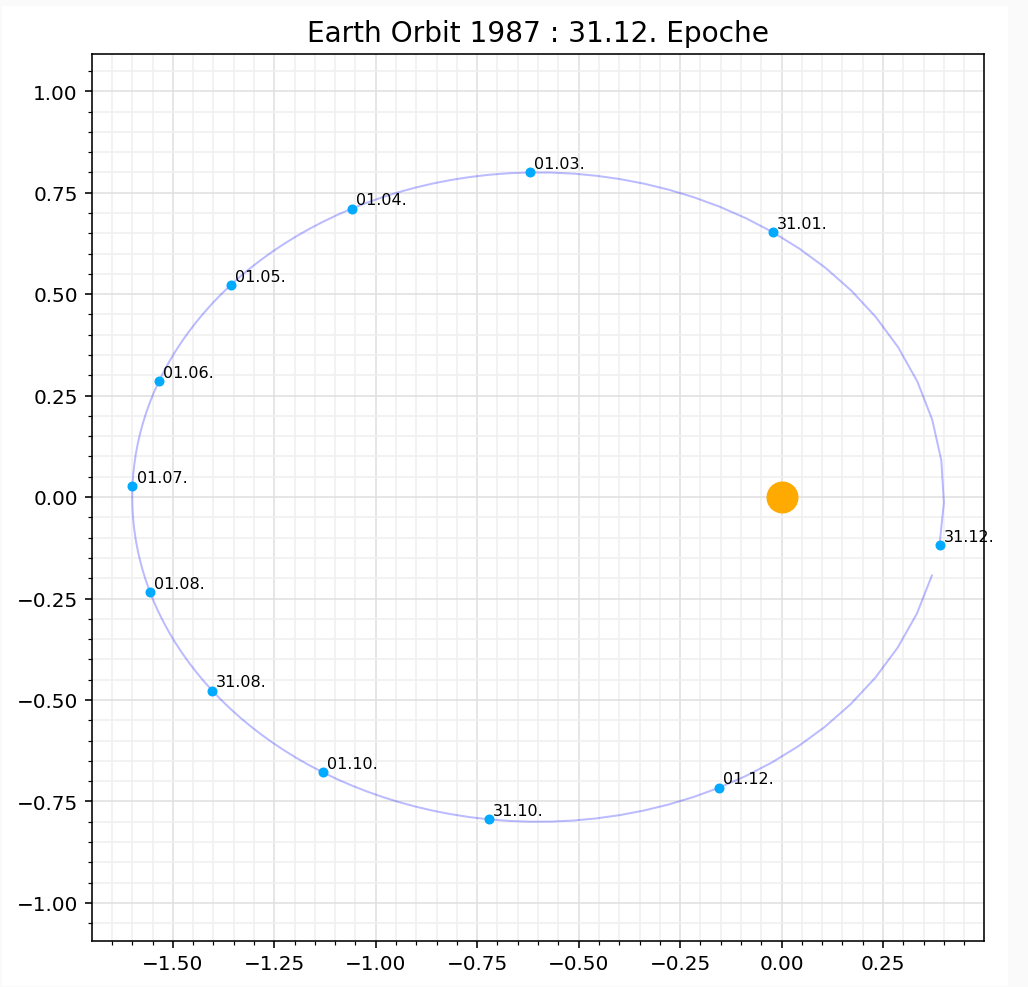
• Erklärt saisonale Effekte: Die Erde bewegt sich im Winter schneller, weil sie näher an der Sonne ist, im Sommer langsamer.

3. Keplersches Gesetz – Das Harmoniegesetz

„Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die Kuben der großen Halbachsen ihrer Bahnen.“

Mathematische Formel:

$\boxed{T^2 \propto a^3}~~$ oder $~~\boxed{\dfrac{T_1^2}{T_2^2} = \dfrac{a_1^3}{a_2^3}}$
wobei:

• $T$ = Umlaufzeit des Planeten um die Sonne
• $a$ = große Halbachse der Ellipse

Erklärung:

• Je weiter ein Planet von der Sonne entfernt ist, desto länger dauert eine Umrundung.
• Dieses Gesetz beschreibt eine mathematische Beziehung zwischen der Bahngröße und der Umlaufzeit.

Bedeutung:

• Es ermöglicht die Berechnung von Planetenbahnen und Umlaufzeiten.
• Zeigt, dass äußere Planeten (z. B. Neptun) viel länger für eine Sonnenumrundung brauchen als innere (z. B. Merkur).
• Dieses Gesetz ist nicht nur auf das Sonnensystem beschränkt, sondern gilt auch für andere Systeme, z. B. Exoplaneten um fremde Sterne oder Monde um Planeten.

Bedeutung der Keplerschen Gesetze in der Wissenschaft

1. Bedeutung für die Astronomie

• Die Keplerschen Gesetze waren ein Meilenstein auf dem Weg zum heutigen heliozentrischen Weltbild.
• Sie widerlegten das geozentrische Modell von Ptolemäus, das auf perfekten Kreisbahnen basierte.
• Sie halfen Isaac Newton, das Gravitationsgesetz zu formulieren, indem sie zeigten, dass Planetenbewegungen durch eine Kraft (Gravitation) bestimmt werden.

2. Bedeutung für die Raumfahrt

• Sie werden bei der Berechnung von Satellitenbahnen verwendet.
• Sie helfen bei der Planung von Raumsonden-Missionen zu anderen Planeten, indem sie die benötigte Geschwindigkeit und Energie vorhersagen.

3. Bedeutung für die allgemeine Physik

• Sie sind eine frühe Anwendung der klassischen Mechanik.
• Sie zeigen, dass physikalische Gesetze mathematisch beschreibbar sind und präzise Vorhersagen ermöglichen.

Kepler-Ellipse und Kepler-Gleichung

• Wikipedia : Kepler-Gleichung
• Ellipse: extrem wichtig zur Bestimmung des Orts eines Planeten in Abhängigkeit der Zeit!
• Kreis: Kepler-Gleichung nicht notwendig